Solving Graphically
Kim Seay
EMAT 6680
Begin with any equation.
I will use 3x-4=11. You can graph both sides of the equation on
the same plane by graphing y=3x-4 and y=11.
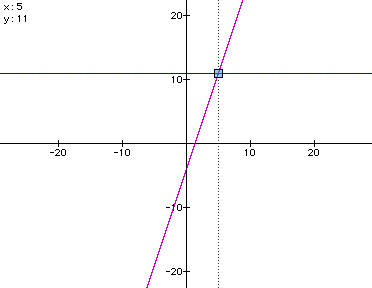The point where the two
lines intersect (which is identified by the square above) is the
solution of the equations. You can see from above that the point
of intersection is (5, 11), and 3(5)-4=11.
Car Rental Quandary
To show students how this
type of information might be useful in every day life, we can
create a scenario involving two car rental stores with different
rates for customers.
Suppose store A charges
an initial fee of $50.00 to rent a car plus an additional $.20
per mile. The charge of this store per mile could be seen by the
graph of y=50+.20x where x= the number of miles.
Store B charges an initial
rental fee of $100.00, but only $.05 per mile. The charge of this
store could be seen by graphing the equation y=100+.05x where
x=number of miles driven.
The question we want to
answer, is when is the final rate charged by the two stores equal?
In other words, for what value of "x" will 50+.20x=100+.05x?
We can solve this by graphing the two equations like we did above.
y = 50 + .20x
y=100 + .05x
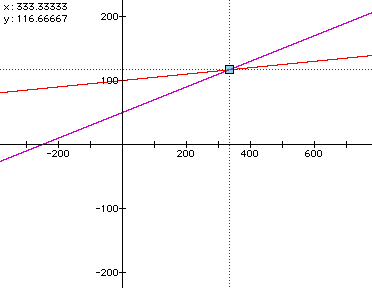The two graphs intersect
approximately at the point (333.33, 116.67). This tells us that
if we drive 333 and one third miles, both car rental stores will
charge $116.67.
Conclusion:
This is something that would
be very easy to demonstrate in the classroom. I think this exploration
would be just as effective with a graphing calculator , and perhaps
more of the students would be able to use that knowledge to help
them solve equations later.
Return