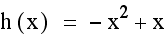This write-up is for problems #3 in Assignment 1.
Linear Functions Tangent to their
Product
by
Brad Simmons
The challenge of this exploration is
to find two linear functions f(x) and g(x) such
that their product
h(x) = f(x).g(x)
is tangent to each of f(x) and
g(x) at two distinct points.
If f(x)
= x and g(x)
= -x+1 and h(x) = (x)(-x+1), then f(x) is tangent
to h(x)
at the origin and g(x) is tangent to h(x) at the point (1, 0 ).
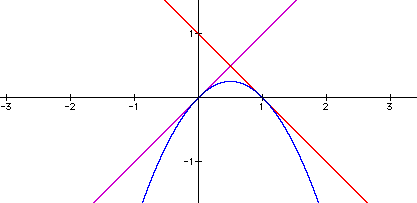
The functions f(x) and g(x) are perpendicular lines.
Since f(x) and g(x) have opposite slopes, their product will result in
a parabola opening downward. We may see this more clearly if we
expand h(x) as seen below.
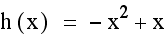
If we explore the possibility of two
functions f(x) and g(x)
both with
positive slopes having a product h(x) that is tangent to each
of f(x) and g(x) at
two distinct points, then it may be helpful to look at the graph
below for f(x) = 4x + 1
and g(x) = x + 3 and
h(x) = (4x + 1)(x + 3).
Not only is h(x) not
tangent to f(x) and g(x), but any relation tangent to f(x) and
g(x) must not fail the vertical line test. This same argument
would hold true for two functions f(x) and g(x) both having negative
slopes.
If we conjecture that the slopes of
f(x)
and g(x)
must be opposites, then we should explore the possibility of f(x) with a
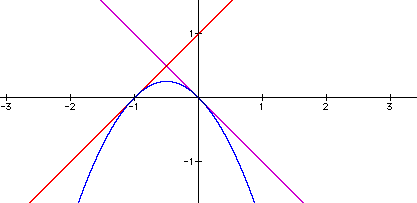
negative slope and g(x) with a positive slope. If f(x) = -x and g(x) = x + 1 and h(x) = (-x)(x
+ 1) then f(x) is tangent to h(x) at the
origin and g(x) is tangent to h(x) at the point ( -1, 0 ).
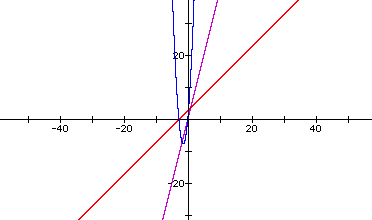
If we let n equal some constant not
equal to zero, then the two linear functions f(x) = nx +n and
g(x) = -nx - (n - 1) have a product h(x) = (nx + n)(-nx - (n - 1)) that is tangent to f(x)
and g(x) in two
distinct points. These two tangent points are the roots of the
function h(x). These tangent points are ( -1 , 0
) and ( -(n-1)/n , 0 ). Furthermore, by using the opposite slopes
in f(x) and g(x) we can arrive at two different functions
f(x) = -nx + n and g(x)
= nx - (n-1) that have
a product h(x) = (-nx +n)(nx
- (n-1)) that is tangent
to f(x) and g(x) in two distinct points. Again these
points are the roots of the function h(x). These
tangent points are ( 1 , 0 ) and ( (n-1)/n , 0 ). The graph below
occurs when n = 4.
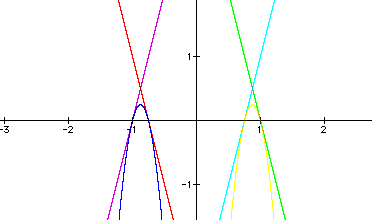
As the absolute value of the slope
increases for f(x) and g(x), these two linear functions approach the vertical
line x = -1. Likewise, as the absolute value of the slope increases
for f(x) and g(x), these two linear functions approach
the vertical line x = 1. To view an animation of the graph directly
above please click
here. Please notice
that when n = 0 we have only one horizontal line at y = 1.
Return