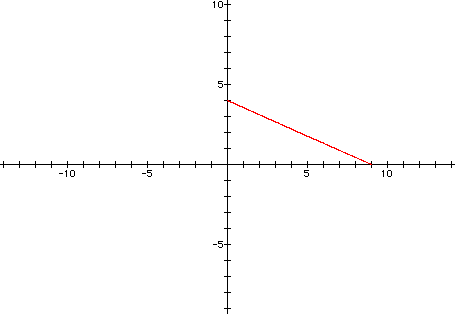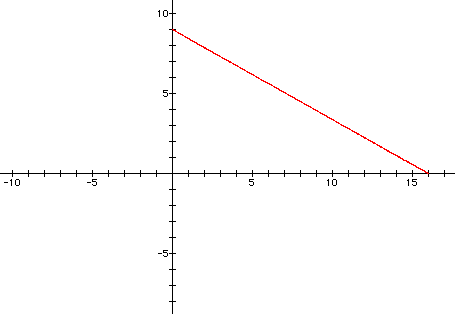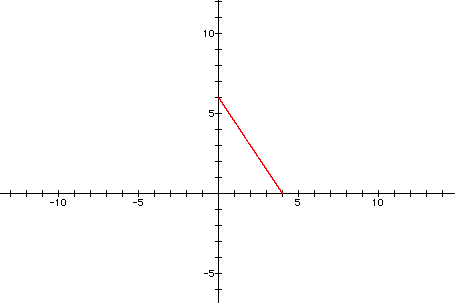This write up is for problems #9 in Assignment
10.
Parametric Curves
by
Brad Simmons
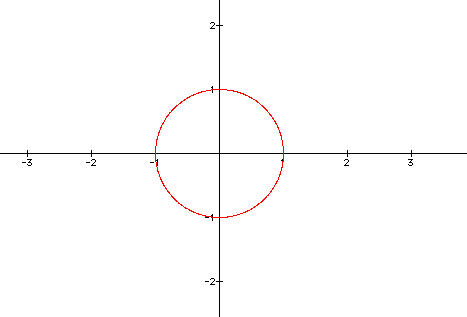
To begin this exploration of parametric
equations we will look at the graph of
x = cos(t)
y = sin(t)
for 0
< t < 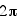
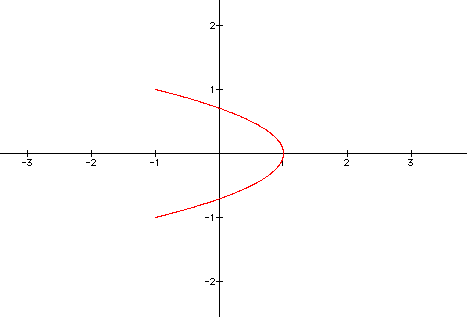
Now if we let the coefficient of t
vary, then we can see how that will effect the graph.
The graph below is for
x = cos(2t)
y = sin(t)
for 0
< t < 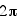
 Now compare the graph for
x = cos(5t)
y = sin(t)
for 0
< t <
Now compare the graph for
x = cos(5t)
y = sin(t)
for 0
< t < 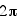
 To continue this exploration of these
parametric curves as the coefficient of t varies in the cosine
function please click
here for a QuickTime movie.
To continue this exploration of these
parametric curves as the coefficient of t varies in the cosine
function please click
here for a QuickTime movie.
How will the graph change if we vary
the coefficient of t in the sine function?
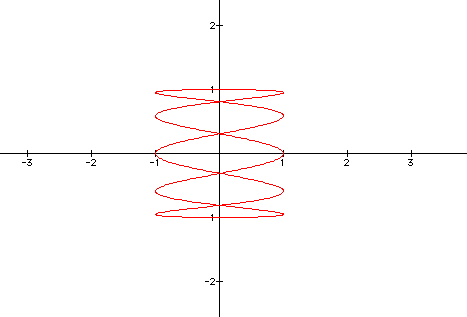
The graph below is for
x = cos(t)
y = sin(2t)
for 0
< t < 
 Now compare the graph for
x = cos(t)
y = sin(5t)
for 0
< t <
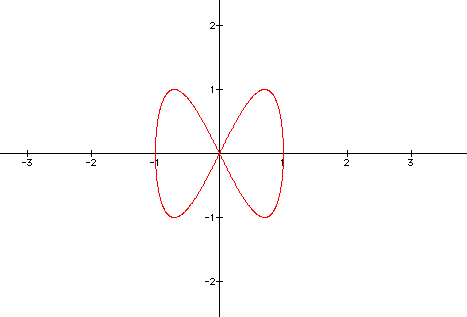
Now compare the graph for
x = cos(t)
y = sin(5t)
for 0
< t < 
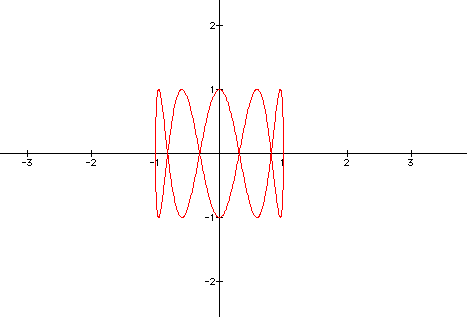
How will the parametric curve change
if we vary the constant by which the cosine or sine function is
multiplied? The parametric equations of the curve can be written
as follows ...
x = a cos(t)
y = b sin(t)
for 0
< t < 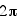
The graph below is for
x = 2 cos(t)
y = 7 sin(t)
for 0
< t < 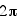
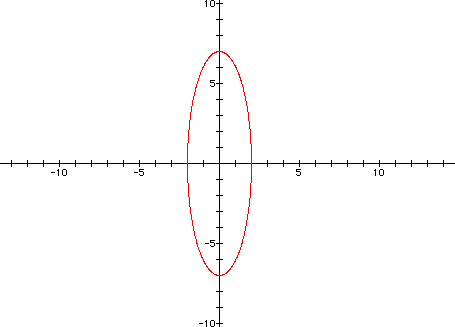 Now compare the graph for
x = 5 cos(t)
y = 7 sin(t)
for 0
< t <
Now compare the graph for
x = 5 cos(t)
y = 7 sin(t)
for 0
< t < 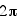
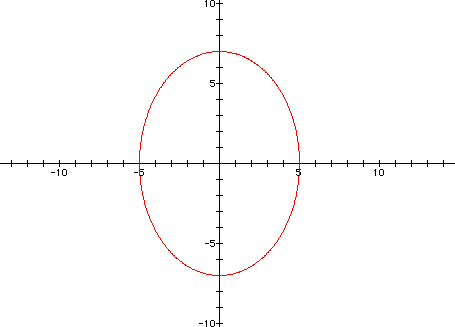 To continue this exploration of these
parametric curves as the constant "a" varies in the
cosine function please click
here for a QuickTime movie.
To continue this exploration of these
parametric curves as the constant "a" varies in the
cosine function please click
here for a QuickTime movie.
How will the graph change if we vary
the constant "b" in the sine function?
The graph below is for
x = 5 cos(t)
y = 3 sin(t)
for 0
< t < 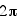
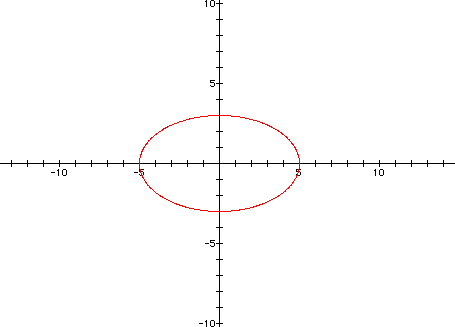 Now compare the graph for
x = 5 cos(t)
y = 8 sin(t)
for 0
< t <
Now compare the graph for
x = 5 cos(t)
y = 8 sin(t)
for 0
< t < 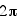
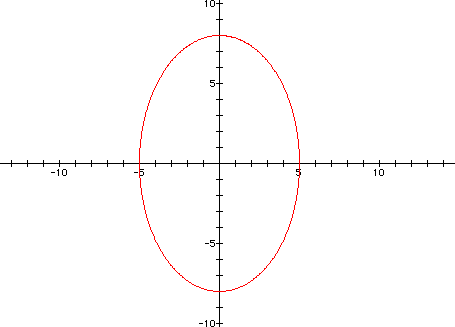 If a > b, then the curve is an ellipse
with a horizontal major axis. If a < b, then the curve is an
ellipse with a vertical major axis. If a = b, then the curve is
a circle with a radius equal to a (or b).
If a > b, then the curve is an ellipse
with a horizontal major axis. If a < b, then the curve is an
ellipse with a vertical major axis. If a = b, then the curve is
a circle with a radius equal to a (or b).
Now we will investigate how the curves
change if each function is squared. Consider the following equations.
x = 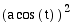 y =
y = 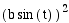 for 0
< t <
for 0
< t < 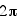
The graph below is for the equations
x =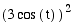 y =
y =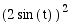 for 0
< t <
for 0
< t < 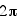
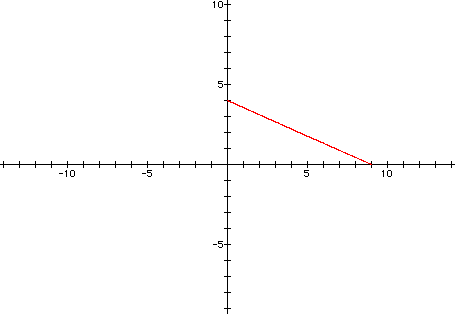 Now compare the graph when the equations
are changed to
x =
Now compare the graph when the equations
are changed to
x =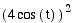 y =
y = for 0
< t <
for 0
< t < 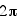
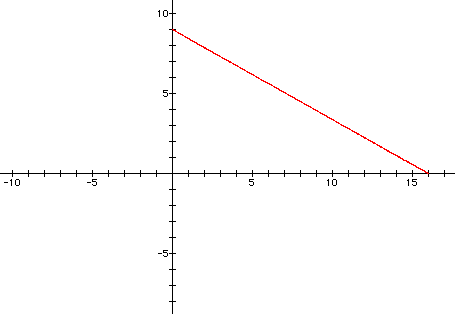 The graph of the curve is a line segment
with endpoints ( 0,
The graph of the curve is a line segment
with endpoints ( 0, 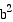 ) and (
) and ( 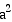 ,
0 ).
,
0 ).
Now consider the equations if the constants
a and b are not squared. What if the equations are changed to
...
x = 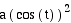 y =
y = 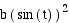 for 0
< t <
for 0
< t < 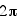
The graph shown below is for a = 4
and b = 6.
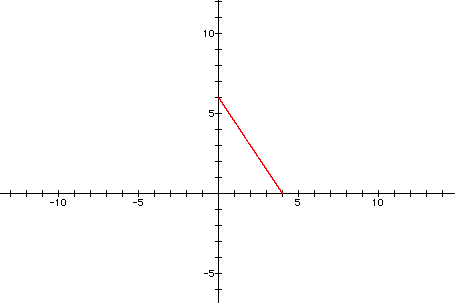 The graph of the curve is a line segment
with endpoints at ( 0, b ) and ( a, 0 ).
The graph of the curve is a line segment
with endpoints at ( 0, b ) and ( a, 0 ).
To take this investigation one step
farther we will look at how the curves change if each function
is cubed. Consider the following equations.
x = 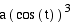 y =
y = 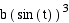 for 0
< t <
for 0
< t < 
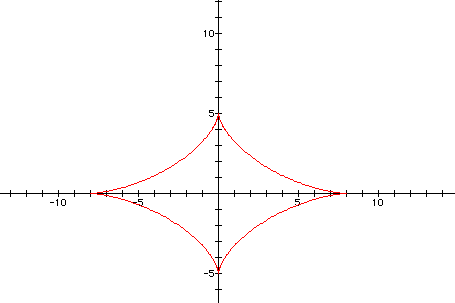
The graph shown below is for a = 7
and b = 5.
 Now consider the graph when a = 4 and
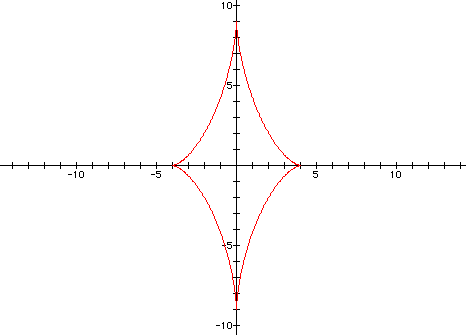
b = 9.
Now consider the graph when a = 4 and
b = 9.
 The graph of the curve is a "diamond
like" curve with the four points of the "diamond"
located at ( a, 0 ), ( -a, 0 ), ( 0, b ), and ( 0, -b).
The graph of the curve is a "diamond
like" curve with the four points of the "diamond"
located at ( a, 0 ), ( -a, 0 ), ( 0, b ), and ( 0, -b).
Return