This write up is for problems #2 in Assignment
11.
Investigating Polar
Equations
by
Kimberly Burrell
and Brad Simmons
Investigation of
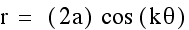In the following graphs we will overlay
the cosine equation in red and the sine equation investigated
above in blue.
When a =1 and k = 1, the polar equations
will produce the following graphs.
At this point, we can observe that
the circular shape has a center at 1 on the polar scale. The cosine
graph (red) is symmetric about the x-axis. This is similar to
the previous sine problem (blue) except the circular graph has
been rotated to the right. If we first allow "a" to
vary we can observe some of the following situations.
When a = 2 and k = 1, the circular
graph has expanded.
Varying "a" in this situation
has the same affect as when we varied "a" in the sine
problem.
Now, we will vary "k" and
hold the "a" constant at 1.
When k > 1, the graph no longer
has a circular shape. It now begins to appear to have pedals.
Such as the following graph with k = 2.
As one can observe from the graphs,
the cosine graph appears to pass through the origin and is rotated
to the right.
Does our theory about the number of
pedals hold true for the cosine problem?
When k =5, the following graph is produced.
Yes, the same theory with "k"
from the sine problem holds true with the cosine problem.
Finally, we will vary both "a"
and "k".
When a = 2 and k = 5, we would expect
the graph to have 5 pedals, to be expanded more than the graph
above, and to be rotated to the right. (See graph below)
We have a graph with 5 pedal-like curves,
expanded from the original graph, and rotated to the right when
compared to the sine graph.
Return