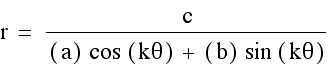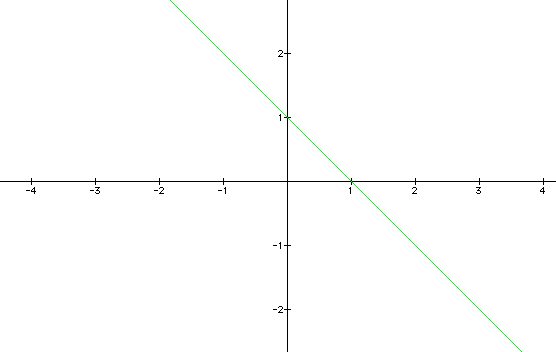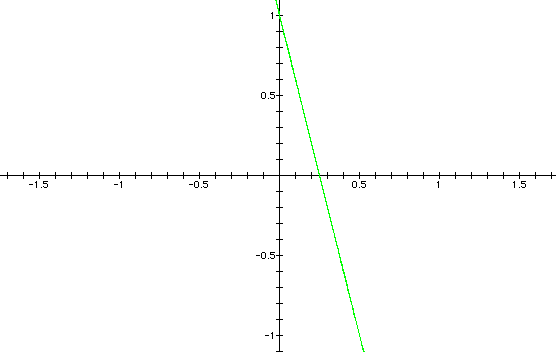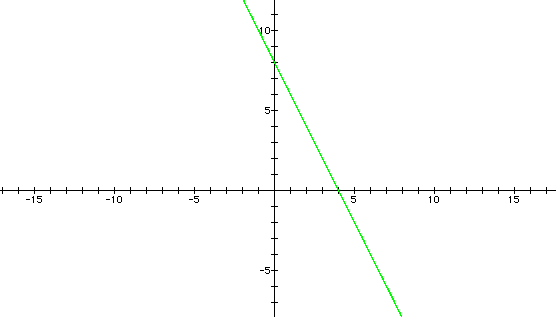This write up is for problems #2 in Assignment
11.
Investigating Polar
Equations
by
Kimberly Burrell
and Brad Simmons
Investigation of
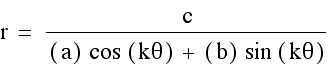 We will begin this part of our investigation
by holding "k", "b" and "c" constant
at 1. We we vary the "a" and look for the change it
makes in the graph of the polar equation.
Let us begin with a = 1
We will begin this part of our investigation
by holding "k", "b" and "c" constant
at 1. We we vary the "a" and look for the change it
makes in the graph of the polar equation.
Let us begin with a = 1
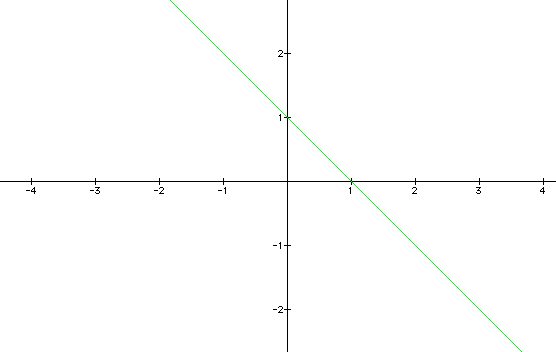 We get a linear graph with the slope
= -1, the y-intercept = 1, and the x-intercept = 1.
Now we will let a =4.
We get a linear graph with the slope
= -1, the y-intercept = 1, and the x-intercept = 1.
Now we will let a =4.
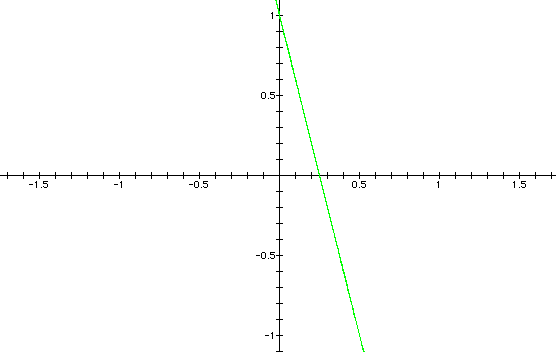 As we see the graph has a y-intercept
still at 1 and the x-intercept is now at 1/4. Could the x-intercept
be determined by the ratio of c/a? If so, is the y-intercept determined
by the ratio of c/b? If we continue to hold "k" constant
at 1, we can vary "a", "b", and "c"
to test our conjecture with regard to the intercepts.
Let c = 80, a = 20, and b = 10.
As we see the graph has a y-intercept
still at 1 and the x-intercept is now at 1/4. Could the x-intercept
be determined by the ratio of c/a? If so, is the y-intercept determined
by the ratio of c/b? If we continue to hold "k" constant
at 1, we can vary "a", "b", and "c"
to test our conjecture with regard to the intercepts.
Let c = 80, a = 20, and b = 10.
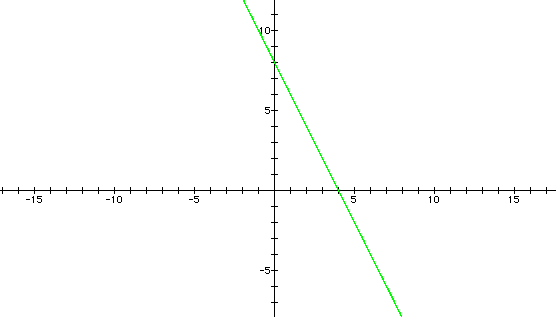 As we see our conjecture holds true
so far. The ratio of c/a = 4 which is the x-intercept. The ratio
of c/b is 8 which is the y-intercept. Although two examples do
not constitute a proof, one more case could be helpful to examine.
Let c = -50, a = 25, and b = -100
As we see our conjecture holds true
so far. The ratio of c/a = 4 which is the x-intercept. The ratio
of c/b is 8 which is the y-intercept. Although two examples do
not constitute a proof, one more case could be helpful to examine.
Let c = -50, a = 25, and b = -100
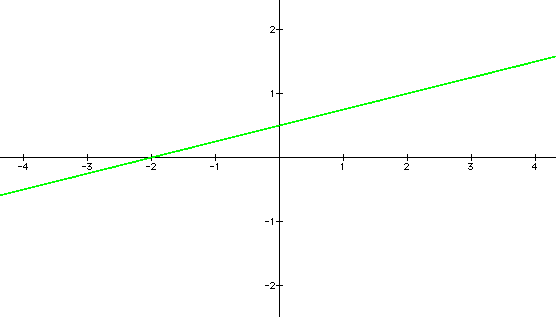 Once again our conjecture holds true.
The ratio of c/a is equal to the x-intercept -2. The ratio c/b
is equal to the y-intercept -1/2.
Now that we have seen how "a",
"b", and "c" can change the graph of this
polar equation, let us investigate what happen when we let "k"
vary.
Let us hold "a", "b",
and "c" constant at 1, and let k = 2.
Once again our conjecture holds true.
The ratio of c/a is equal to the x-intercept -2. The ratio c/b
is equal to the y-intercept -1/2.
Now that we have seen how "a",
"b", and "c" can change the graph of this
polar equation, let us investigate what happen when we let "k"
vary.
Let us hold "a", "b",
and "c" constant at 1, and let k = 2.
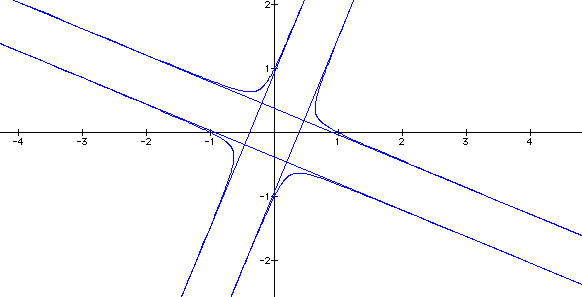 The graph is a rectangle (maybe a square)
that appears to have center at the origin. The extended side of
the rectangle form asymptotes of what appears to be four parabolas.
What happens if we let k = 3?
The graph is a rectangle (maybe a square)
that appears to have center at the origin. The extended side of
the rectangle form asymptotes of what appears to be four parabolas.
What happens if we let k = 3?
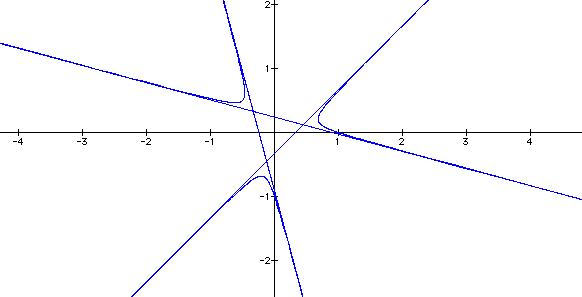 This time the polygon is a triangle
and its extended sides form the asymptotes of what appears to
be three parabolas.
Can we make a similar conjecture to
that of the pedals in the polar equation at the beginning of this
write up? If k is an odd number, then the graph will be that of
a polygon with k sides whose extended sides form the asymptotes
for number of parabolas that is equal to k. Furthermore, if k
is an even number, then the graph will be that of a polygon with
2k sides whose extended sides form the asymptotes for number of
parabolas that is equal to 2k.
To test this conjecture and possibly
explore this topic further please click
here for a QuickTime for in which we will let k vary.
Finally, we will let c = 8, a = 4,
b = 2 and k = 5.
This time the polygon is a triangle
and its extended sides form the asymptotes of what appears to
be three parabolas.
Can we make a similar conjecture to
that of the pedals in the polar equation at the beginning of this
write up? If k is an odd number, then the graph will be that of
a polygon with k sides whose extended sides form the asymptotes
for number of parabolas that is equal to k. Furthermore, if k
is an even number, then the graph will be that of a polygon with
2k sides whose extended sides form the asymptotes for number of
parabolas that is equal to 2k.
To test this conjecture and possibly
explore this topic further please click
here for a QuickTime for in which we will let k vary.
Finally, we will let c = 8, a = 4,
b = 2 and k = 5.
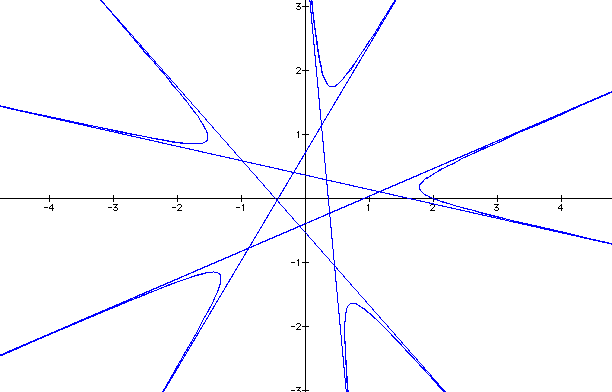 The polygon has 5 sides as we might
suspect since k = 5. How do the values of "c", "a",
and "b" effect the intercepts of the extended sides
of the polygon? Is there a relationship involving "c",
"a", "b", and the vertex of each parabola?
If there is a relationship, can a definite ratio be established
similar to the linear graphs presented at the beginning of this
part of our investigation?
The polygon has 5 sides as we might
suspect since k = 5. How do the values of "c", "a",
and "b" effect the intercepts of the extended sides
of the polygon? Is there a relationship involving "c",
"a", "b", and the vertex of each parabola?
If there is a relationship, can a definite ratio be established
similar to the linear graphs presented at the beginning of this
part of our investigation?
Return