
This is a write up for problem #6 from assignment 2.
Exploration of a Parabola
By
Brad Simmons
If we begin our exploration of a parabola
with the second degree equation
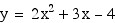 we can examine its graph which appears
below.
we can examine its graph which appears
below.
 This is a parabola with its vertex
in the third quadrant and it is concave up.
This is a parabola with its vertex
in the third quadrant and it is concave up.
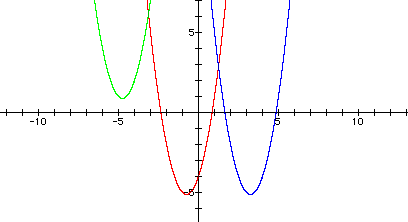
If we overlay a new graph replacing
each x with ( x - 4 ), then we can see how the vertex is shifted
4 units to the right. Our original equation appears in red and
our new equation appears in blue
in the graph below.
 It may be helpful to look at the equation
of our blue graph.
It may be helpful to look at the equation
of our blue graph.

If we explore the possibility
of moving the graph of our parabola into the second quadrant we
need to move its vertex to the left and up. Since replacing x
with ( x - 4 ) in the equation of the red graph moved
its vertex to the right, then replacing x with ( x + 4 ) should
move its vertex to the left. Furthermore, replacing the constant
term (-4) with (+2) in the equation of the red graph moves
the vertex of our parabola up. If we overlay the new graph colored
green we see it is in the second quadrant.
 Now compare the equations of all three
parabolas.
Now compare the equations of all three
parabolas.
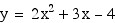 Red Parabola
Red Parabola
 Blue Parabola
Blue Parabola
 GREEN
Parabola
GREEN
Parabola
To view these equation in expanded form please click
here.
It would be logical
to change our equation to produce a graph that shares the same
vertex and is concave down. If we overlay the graph of the following
equation in black, then we can see all four parabolas together.

 Notice the green and black parabolas share the same vertex and the black
parabola is concave down. Now if we expand the equation of this
black parabola we can compare it to the expanded equations of
our other three parabolas.
Notice the green and black parabolas share the same vertex and the black
parabola is concave down. Now if we expand the equation of this
black parabola we can compare it to the expanded equations of
our other three parabolas.
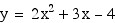 Red
Parabola
Red
Parabola
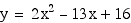 Blue
Parabola
Blue
Parabola
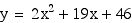 Green Parabola
Green Parabola
 Black Parabola
Black Parabola
In reaching this point
in our exploration, we may want to have our students complete
the square for each of the equations above in order to write the
equations in the form

Return





