This write up is for problems #12 in Assignment 4.
Concurrency of Perpendicular Bisectors
of a Triangle
by
Brad Simmons
In this write up we will prove that
the three perpendicular bisectors of the sides of a triangle are
concurrent.
To review the definition of perpendicular
bisector of a segment and concurrent please click
here.
Given:
Triangle ABC with perpendicular bisectors r, s, t
Prove: lines
r, s, t are concurrent in a point O and that OA = OB = OC
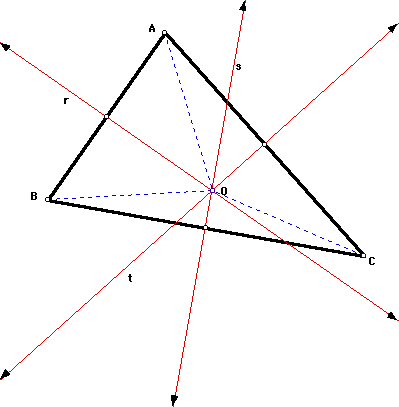1. It
is given that line r is the perpendicular bisector of segment
AB.
2. It
is also given that line s is the perpendicular bisector of segment
BC.
3. Since
segments AB and BC are not parallel, then lines r and s are not
parallel. Therefore, lines r and s intersect in a point O.
4. Since
a point on a perpendicular bisector is equidistant from the endpoints,
then OA=OB and OB=OC.
5. By
the transitive property of equality, OA=OC
6. Point
O is on the perpendicular bisector ( line t ) of segment AC because
a point equidistant from two points is on the perpendicular bisector
of the segment determined by those points.
7. Therefore,
from statement 3,4, 5, and 6 it has been proved that Point O lies
on lines r, s, and t. Likewise, OA = OB = OC.
For a dynamic sketch that can be manipulated
please click
here.
Return