This write-up is for problems #7 in Assignment
6.
Constructing Common Tangents to
Circles
by
Brad Simmons
In this write-up we will attempt to
contstruct the common tangents to two given circles.
A line is tangent to a circle
if it intersects the circle in just one point.
A line that is tangent to each of two
coplanar circles is called a common tangent.
Common intermal tangents intersect the segment joining the centers of the two
circles.
Common extermal tangents do not intersect the segment joining the centers of
the two circles.
If we begin with two circles that are
tangent to each other, we must examine two different cases. One
circle could be inside of the other circle. The two circles would
be internally tangent. In this case, we will have only one line
that is tangent to both circles. The point of tangency will be
where the two cirlces and the one common external tangent
intersect. The image below is an example of such a case.
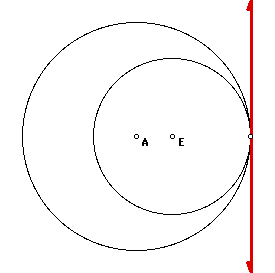
The construction of this common
external tangent shown above is a relatively simple task.
A line is tangent to a circle if the line is perpendicular to
the radius drawn to the point of tangency. The centers of the
two circles as well as the point of tangency ( of the circles)
are colinear. Therefore, by constructing a line perpendicular
to the line which contians the two centers and point of tangency
(of the circles) at the point of tangency ( of the circles), we
have constructed our common external tangent.
Furthermore, the two circles could
be externally tangent as shown in the image directly below. In
this case there will be one common internal tangent. The
point of tangency will be where the two circles and the common
intermal tangent intersect.
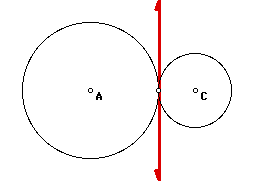
The construction of the common internal
tangent shown above is similar to the common external tangent
previously described. Construct a line perpendicular to the segment
that joins the center of the two circles at the point of tangency
(of the circles). The common internal tangent will be perpendicular
to the radius of each of our two circles.
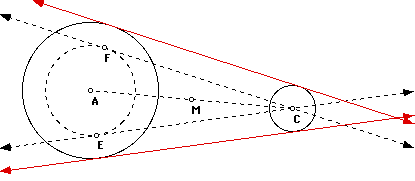
The externally tangent circles will
also have two common external tangents as shown below.
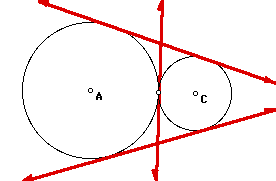
The construction of the two common
external tangents requires a little more descussion than our
first two constructions. It is possible to construct a tangent
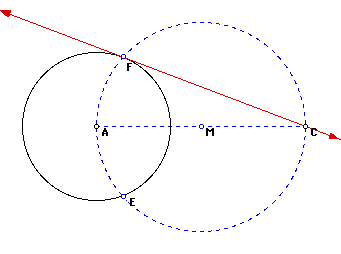
to a circle from a point outside the circle. This is done by constructing
the midpoint of the segment that joins the center of the circle
(point A) and our point C outside the circle. Then construct a
circle with its center at our midpoint M with a radius congruent
to the segment MC. The points of intersection of our original
circle A and our constructed circle M will be the points of tangency.
We can then construct a tangent line from our point C outside
the circle passing through the point of tangency on our circle
A. (There will be two such tangent lines. These tangent lines
are line CF and line CE). This construction is illistrated below.
The red line CF is tangent to circle A and passes through point
C.
In constructing the two common external
tangents, the construction described above is very helpful
if we reduce the size of the radius of both of our given circles
by equal amounts so that our smaller circle is reduced to a point.
The line constructed througth our point C (center of the smaller
original circle) and tangent to our smaller constructed circle
(inside the larger original circle) will be parallel to the common
external tangent.
For a dynamic sketch that can be manipulated
please click
here.
For a GSP script that will contruct
the common external tangents for two given circles please
click
here.
Geometer's Sketchpad 4.0 users please click
here.
The next logical step is to consider
two given circles that have four common tangents.
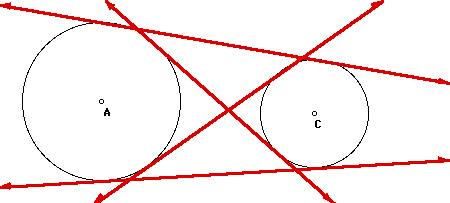In this case, there are two common
external tangents and two common internal tangents.
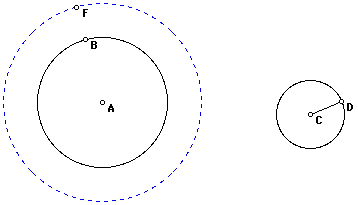
The construction for the common
intermal tangents is similar to that of the construction of
the common extermal tangents. In order to construct
the common external tangents we reduced the length of the
radius of our smaller circle C to the extent that it became a
point C. We then constructed a smaller circle with its center
at point A inside our larger circle A. The radius of this newly
constructed circle has a radius equal to the radius of circle
A (the original larger circle) minus the radius of circle C (the
original smaller circle). To construct the common internal
tangent, construct a new circle with its center a point A
and a radius equal to the radius of our original circle A plus
the radius of our original circle C. The length of AF is equal
to the lenght of AB plus the length of CD.
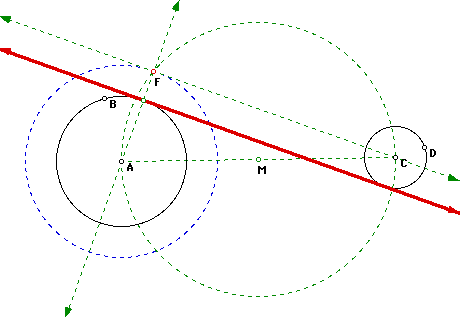
If we now construct a line passing
through point C and tangent to our newly constructed circle (blue
dashed circle), it will be parallel to one common internal
tangent of our given circles. (black circle A and black circle
C).
For a dynamic sketch that can be manipulated
please click
here.
For a GSP script that will contruct
the common internal tangents for two given circles please
click
here.
Geometer's Sketchpad 4.0 users please click
here.
Return