This write-up is for Assignment 7.
Tangent Circles
by
Brad Simmons
Given two circles and a point on one
of the circles it is possible to construct a circle tangent to
the two circles with one point of tangency being the designated
point.
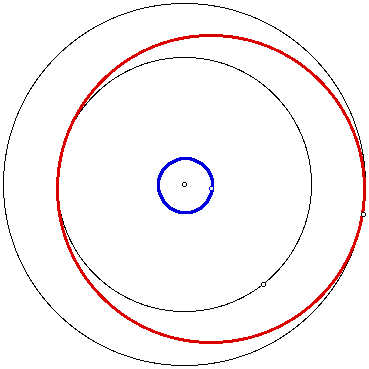
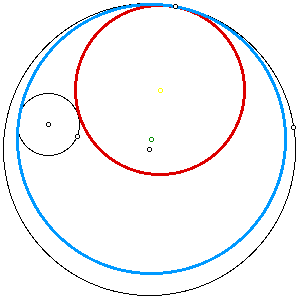In the image above, the given circles
are in black. Hence, we have been able to construct two different
circles that satisfy the constraints of our problem. The red circle
and the light blue circle are both tangent to the given circles
with one point of tangency being a designated point on our larger
black circle.
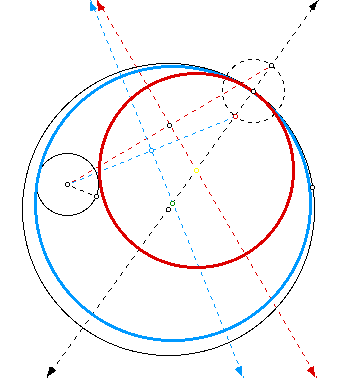
If we examine our construction below,
the red dashed segment is the base of an isosceles triangle. The
length of the two congruent sides of this isosceles triangle is
equal to the radius of our red tangent circle plus the radius
of our smaller given circle. The light blue tangent circle was
constructed in a similar way. However, the length of the congruent
sides of the isosceles triangle in this construction is equal
to the radius of the light blue circle minus the radius of our
smaller given circle. Notice that the center of the tangent circle
is on the perpendicular bisector of the base of the isosceles
triangle mentioned above. The center of the tangent circle is
also on the line which passes through the center of the larger
given (black) circle and the designated point on the larger given
circle.
If we animate the sketch above and
trace the centers of our red and light blue tangent circles, we
see that the locus of the center of each tangent circle form an
ellipse. For a GSP sketch with animation please click
here.
In the case of our red tangent circle,
our smaller given circle is external to the "red" tangent
circle. For a GSP script that will produce this result please
click
here.
Geometer's Sketchpad 4.0 users please click
here.
Click here for a GSP sketch
with the designated point on the smaller circle.
In the case of our light blue tangent
circle, our smaller given circle is internal to the "light
blue" tangent circle. For a GSP script that will produce
this result please click
here.
Geometer's Sketchpad 4.0 users please click
here.
Click here for a GSP sketch
with the designated point on the smaller circle.
By using the three GSP sketches that
are linked above, it is possible to explore how the locus of centers
of the constructed tangent circle behave.
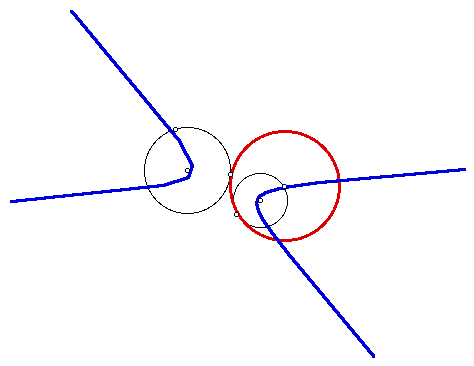
Please look at the image below. When
the designated point on the larger black circle is animated around
the larger black circle, the locus (blue image) of the center
of red tangent circle forms a hyperbola.
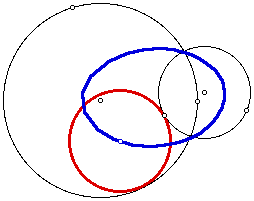
If the two given (black) circles intersect,
the locus (blue) of the center of the red tangent circle forms
an ellipse as the designated point moves around the smaller (black)
circle.
If the smaller (black) given circle
is moved inside the larger (black) given circle, an ellipse is
formed by the locus (blue) of the center of the red tangent circle
as the designated point moves around the smaller (black) circle.
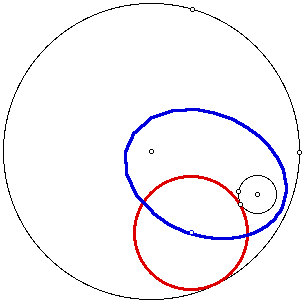
If the two given (black) circles have
the same center, the locus (blue) of the center of the red tangent
circle forms a circle as the designated point moves around the
smaller (black) circle.
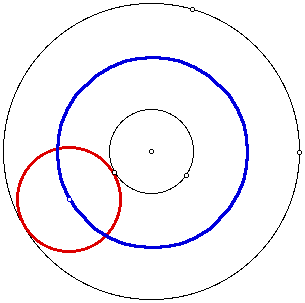
In the previous four examples, the
path of our designated point has been around the circle external
to our red tangent circle. Now, look at the next three examples.
Compare and contrast these three examples with the four we have
just examined. Feel free to go back to the GSP sketch links above
in order to manipulate the given circles.
The locus (blue) of the center of the
red tangent circle forms an ellipse when then designated point
moves around the larger (black) circle.
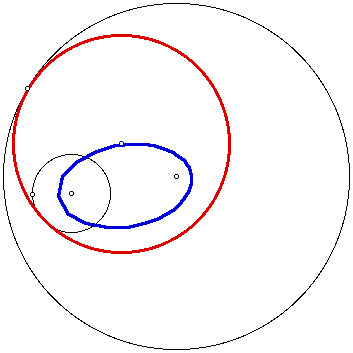
In the image below, both given (black)
circles are internal to the red tangent circle. The locus (blue)
of the center of the red tangent circle forms a hyperbola.
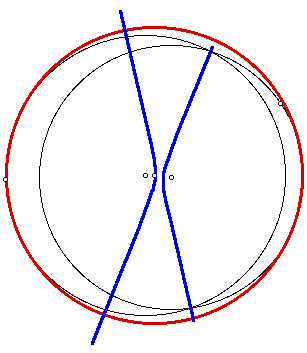
In the next example, the two given
(black) circles share the center point. As the designated point
moves around the larger (black) circle, the locus (blue) of the
center of the red tangent circle forms a circle.
Return