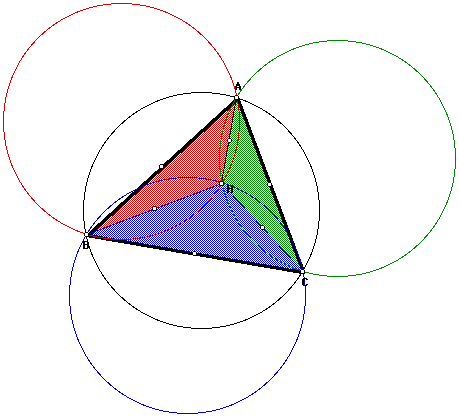Assign1

This write up is for problems Assignment 8.

Altitudes and Orthocenters

Brad Simmons

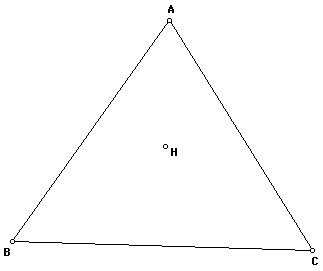
To begin our exploration and discussion, we construct the orthocenter (H) of triangle ABC. The orthocenter of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the opposite side of the triangle.

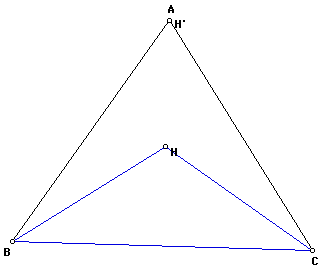
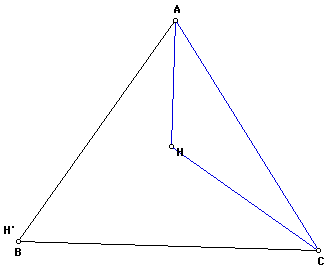
We can construct the orthocenter ( H') of triangle HBC. The image below shows H' and point A coincide.

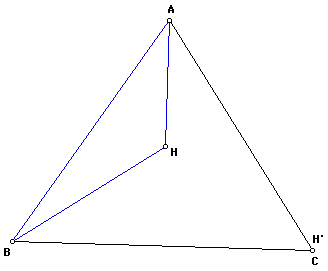
We can construct the orthocenter ( H') of triangle HAB. The image below shows H' and point C coincide.

We can construct the orthocenter ( H') of triangle HAC. The image below shows H' and point B coincide.

For a GSP sketch that can be manipulated please click here.

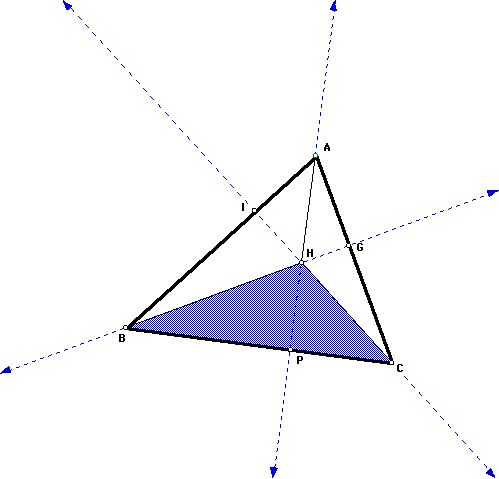Given: point H is the orthocenter of triangle ABC

Prove: point A is the orthocenter of triangle HBC

1. Segment AP is an altitude of triangle ABC since line AP passes through the orthocenter H of triangle ABC.

2. Segment AP is perpendicular to segment BC because an altitude is a segment that joins a vertex with the opposite side of a triangle and is perpendicular to that opposite side.

3. Angle APB is a right angle because segment AP is perpendicular to segment BC.

4. Point H lies on segment AP because an altitude of a triangle passes through the triangle's orthocenter.

5. Angle HPB is a right angle because segment HP is perpendicular to segment BC.

6. Segment HP is an altitude of triangle HBC since it is a segment perpendicular to side BC and passing through the vertex H.

7. Points A, H, and P are collinear because the orthocenter H lies on the altitude AP.

8. Point A lies on the extension of the altitude HP. (Altitude HP of triangle HBC).

9. Segment BG is an altitude of triangle ABC since it passes through the orthocenter H of triangle ABC.

10. Segment BG is perpendicular to segment AC because an altitude is a segment that joins a vertex with the opposite side of a triangle and is perpendicular to that opposite side.

11. Points B, H, G are collinear because the orthocenter H lies on the altitude BG.

12. Angle HGC is a right angle because segment AC is perpendicular to segment BG.

13. Segment CG is an altitude of triangle HBC since it is a segment perpendicular to the extension of side BH (at point G) and passing through the vertex C.

14. Point A lies on the extension of the altitude CG since points A, C, and G are collinear.

15. By similar reasoning it can be proved that Point A lies on the extension of segment BI which is an altitude of triangle HBC.

16. Point A is the orthocenter of triangle HBC since it is the common intersection of the lines containing the three altitudes of triangle HBC.

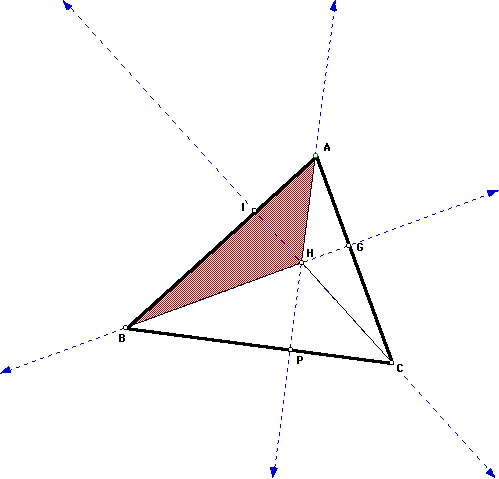
By similar reasoning it can be proved that Point B is the orthocenter of triangle HAC.

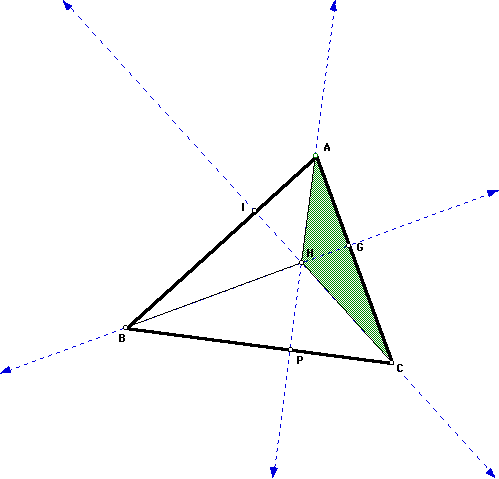
Furthermore, by similar reasoning it can be proved that Point C is the orthocenter of triangle HAB.

Now if we construct the circumcircles of triangles ABC, HBC, HAB, and HAC as shown below, we can explore the behavior of the circumcircles if we manipulate the orthocenter (H) or and of the vertices of triangle ABC. If we drag the point H out to where the point C is now located, then point C will move to where point H is now located and the red circumcircle and black circumcircle will switch places as well. (Try this by clicking on the GSP sketch link below this image.) Furthermore, if we move point H out to the location of point A, then the black circumcircle and blue circumcircle will switch places. What will happen if we move point H out to the location of point B? Will the black circumcircle and green circumcircle switch places?

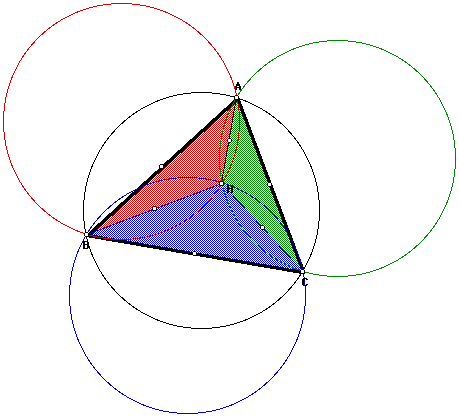
For a GSP sketch that can be manipulated please click here.

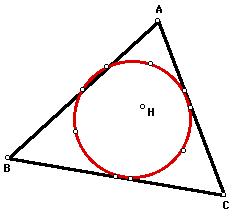
The image below shows the nine point circle (red) and orthocenter (H) of triangle ABC.

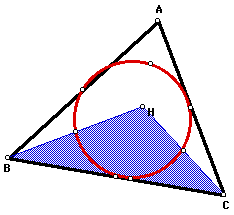
Now look at the nine point circle (red) of triangle HBC.

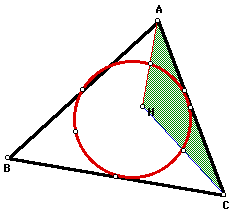
Now look at the nine point circle (red) of triangle HAC.

Is this nine point circle (red) also the same for triangle HAB?

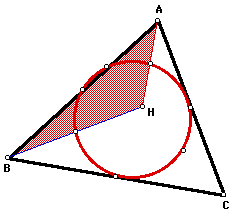
It appears from the images above that all four triangles ABC, HBC, HAC, and HAB share the same nine point circle. With the help of GSP we can construct the nine point circle for all four triangles in the same sketch and then manipulate the sketch to examine other acute, obtuse or right triangles.

For a GSP sketch that can be manipulated please click here.

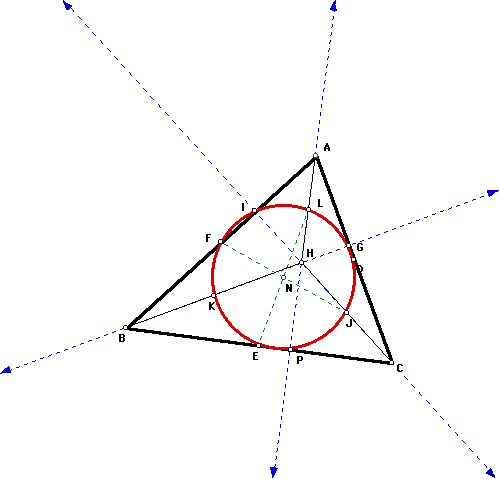Given: point H is the orthocenter of triangle ABC.

Prove: triangle ABC and triangle HBC share the same nine point circle.

1. For triangle ABC, point L is the midpoint of the segment from vertex A to the orthocenter H. For triangle HBC, point L is the midpoint of the segment from vertex H to the orthocenter A.

2. For triangle ABC, point K is the midpoint of the segment from vertex B to the orthocenter H. For triangle HBC, point K is the midpoint of side HB.

3. For triangle ABC, point J is the midpoint of the segment from vertex C to the orthocenter H. For triangle HBC, point J is the midpoint of side HC.

4. For triangle ABC, point I is the foot of the altitude CI. For triangle HBC, point I is the foot of the altitude BI.

5. For triangle ABC, point P is the foot of the altitude AP. For triangle HBC, point P is the foot of the altitude HP.

6. For triangle ABC, point G is the foot of the altitude BG. For triangle HBC, point G is the foot of the altitude CG.

7. For triangle ABC, point D is the midpoint of the side AC. For triangle HBC, point D is the midpoint of the segment from vertex C to the orthocenter A.

8. For triangle ABC, point F is the midpoint of the side AB. For triangle HBC, point F is the midpoint of the segment from vertex B to the orthocenter A.

9. For triangle ABC, point E is the midpoint of the side BC. For triangle HBC, point E is the midpoint of the side BC.

10. The points L, K, J, I, P, G, D, F, and E are points used to construct the nine point circle for both triangle ABC and triangle HBC.

By similar reasoning it can be proved that triangle HAB and triangle HAC also share this same nine point circle.

Return