
This write up is for Assignment 9.
Pedal Triangles
by
Brad Simmons
To begin our exporation and discussion
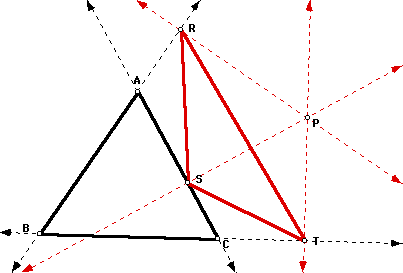
of pedal triangles, we will examine the construction of a pedal
triangle. The point P is a point in the same plane as triangle
ABC. The (red) pedal triangle RST for triangle ABC and pedal point
P is shown in the image below. By constructing perpendiculars
to each side of triangle ABC that pass through the pedal point
P, we can locate the vertices of the pedal triangle RST. The vertices
of the pedal triangle are located at the intersection points of
the (red) perpendicular lines and the sides (or the extention
of the sides) of triangle ABC.
 For a GSP sketch that can be manipulated
please click
here.
For a GSP script to construct a pedal
triangle to triangle ABC please click
here.
Geometer's Sketchpad 4.0 users please click
here.
For a GSP sketch that can be manipulated
please click
here.
For a GSP script to construct a pedal
triangle to triangle ABC please click
here.
Geometer's Sketchpad 4.0 users please click
here.
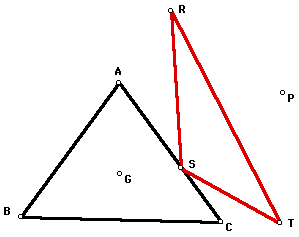
It may be interesting to look at the
pedal triangle of triangle ABC if the pedal point P is located
at a particular specified point such as the centroid. In other
words, the pedal point P is the centroid of triangle ABC. The
image below shows the centroid (G) of triangle ABC and the pedal
triangle RST with the pedal point P outside of triangle ABC.
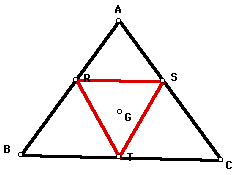
Now if the pedal point is the centroid
(G), then the vertices of the pedal triangle RST appear to be
located on the sides of triangle ABC. The point T also appears
to be the midpoint of segment BC.
 To explore the conjectures made above
or any other conjectures that could be made, please click
here for a GSP sketch that can be manipulated.
To explore the conjectures made above
or any other conjectures that could be made, please click
here for a GSP sketch that can be manipulated.
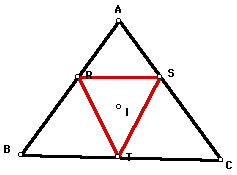
If the pedal point P is the Incenter
(I) of triangle ABC, then the pedal triangle RST appears to be
the same a the image above.
 For a GSP sketch that can be manipulated
please click
here.
For a GSP sketch that can be manipulated
please click
here.
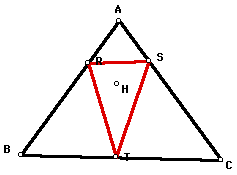
If the pedal point P is the orthocenter
(H), then the (red) pedal triangle looks similar.
 For a GSP sketch that can be manipulated
please click
here.
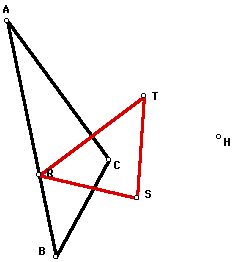
If triangle ABC is manipulated so the
orthocenter (H) is outside triangle ABC, the pedal triangle RST
for the pedal point H appears to have one vertex R on one side
AB (see the image below). Will one vertex of the pedal triangle
always be located on at least one side of triangle ABC?
For a GSP sketch that can be manipulated
please click
here.
If triangle ABC is manipulated so the
orthocenter (H) is outside triangle ABC, the pedal triangle RST
for the pedal point H appears to have one vertex R on one side
AB (see the image below). Will one vertex of the pedal triangle
always be located on at least one side of triangle ABC?
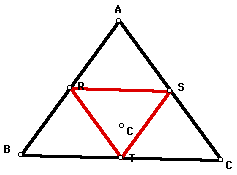
Now if we move the pedal point of triangle
ABC to the circumcenter of ABC, then the (red) pedal triangle
once again appears to have its vertices R, S, T located on the
sides of triangle ABC.
 For a GSP sketch that can be manipulated
please click
here.
If triangle ABC is manipulated so its
circumcenter (C) is outside of triangle ABC, then the pedal triangle
RST for the pedal point C still appears to have its vertices R,
S, T located on the sides of triangle ABC (see the image below).
For a GSP sketch that can be manipulated
please click
here.
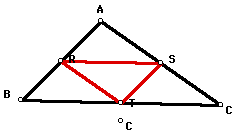
If triangle ABC is manipulated so its
circumcenter (C) is outside of triangle ABC, then the pedal triangle
RST for the pedal point C still appears to have its vertices R,
S, T located on the sides of triangle ABC (see the image below).
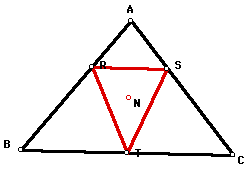
The image below shows triangle ABC
and the pedal triangle RST for the pedal point N. The point N
is the center of the nine point circle for triangle ABC.
 For a GSP sketch that can be manipulated
please click
here.
For a GSP sketch that can be manipulated
please click
here.
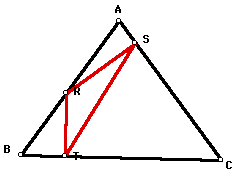
Now that we have explored moving the
pedal point to the different centers of triangle ABC, it may be
interesting to move the pedal point to one of the sides of triangle
ABC. The image below shows the pedal triangle RST for triangle
ABC when the pedal point P is on side AB.
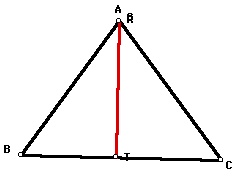
 When the pedal point is moved to vertex
A, then the (red) pedal triangle degenerates to a line segment
AT. This line segment is called the Simson Line.
When the pedal point is moved to vertex
A, then the (red) pedal triangle degenerates to a line segment
AT. This line segment is called the Simson Line.
 For a GSP sketch that can be manipulated
please click
here.
For a GSP sketch that can be manipulated
please click
here.
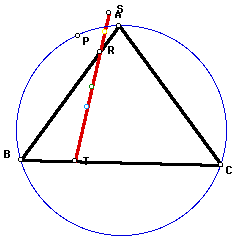
If the circumcircle (blue) is constructed
for triangle ABC, then we can see that the Simson Line is formed
when the pedal point P lies on the the circumcircle.
 If we locate the midpoints of the three
sides of the pedal triangle, then we can examine the locus of
each midpoint as the pedal point P moves around the circumcircle.
If we locate the midpoints of the three
sides of the pedal triangle, then we can examine the locus of
each midpoint as the pedal point P moves around the circumcircle.
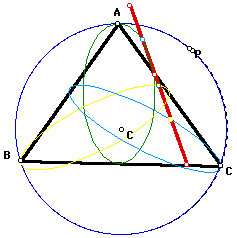 Does each median of triangle ABC lie
on the major axis of an ellipse formed by the locus of a midpoint
of a side of the pedal triangle for pedal point P when P moves
around the circumcircle of triangle ABC?
For a GSP sketch that can be manipulated
please click
here.
Does each median of triangle ABC lie
on the major axis of an ellipse formed by the locus of a midpoint
of a side of the pedal triangle for pedal point P when P moves
around the circumcircle of triangle ABC?
For a GSP sketch that can be manipulated
please click
here.
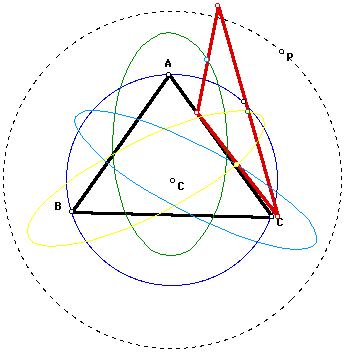
If we move the pedal point P around
a circle (black dashed circle) with its center at the circumcenter
of triangle ABC and its radius larger than that of the circumcircle
of triangle ABC, the locus of the three midpoints of the sides
of the (red) pedal triangle can be examined. How do they compare
to the locus of midpoints observed above?
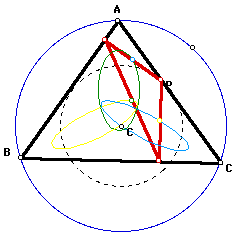
 Now what if we move the pedal point
P around a circle (black dashed circle) with its center at the
circumcenter of triangle ABC and its radius smaller than that
of the circumcircle of triangle ABC. The locus of the midpoints
of the sides of the (red) pedal triangle are elliptical. Will
this always be the case? (see the image
below)
Now what if we move the pedal point
P around a circle (black dashed circle) with its center at the
circumcenter of triangle ABC and its radius smaller than that
of the circumcircle of triangle ABC. The locus of the midpoints
of the sides of the (red) pedal triangle are elliptical. Will
this always be the case? (see the image
below)
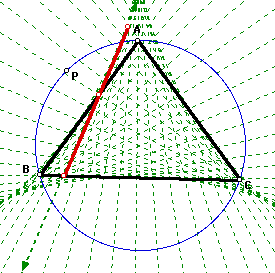
The image below can be constructed
if we trace the extention of the simson line as the pedal point
P moves around the circumcirle of triangle ABC.
 For a GSP sketch that can be manipulated
please click
here.
For a GSP sketch that can be manipulated
please click
here.
Is there a point on the circumcircle
for pedal point P that has side AC as its Simson line? What about
AB as its Simson line? What about BC as its Simson line?
For a GSP sketch that may help answer
these questions please click
here.
Return

















