EMAT 6690

Essay 2

Pedal Triangles and Similarity

by Kimberly Burrell, Brad Simmons, and Doug Westmoreland

If we have a triangle ABC and a point P, we can begin to construct the pedal triangle of triangle ABC for the pedal point P by constructing a line perpendicular to a side of the triangle and passing through the pedal point P. Likewise, if we now construct perpendiculars to the other two sides and also passing through the pedal point P, then we will have three points of intersection. If we connect these three intersection points ( intersection of the perpendiculars with its respective side of triangle ABC) with segments, then we have the pedal triangle for triangle ABC and pedal point P.

For a GSP script that can be used to construct a pedal triangle please click here.

Geometer's Sketchpad 4.0 users please click here.

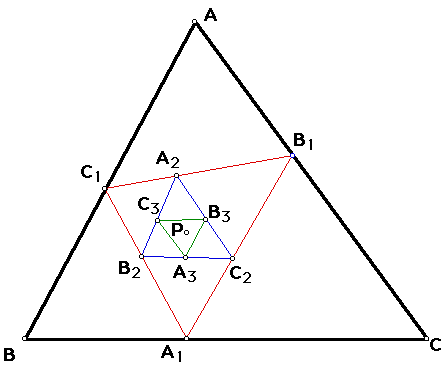
Consider triangle ABC and a point P located inside the triangle. Construct the red pedal triangle A1B1C1. Now using the same pedal point P, construct the pedal triangle for A1B1C1. This is the blue triangle A2B2C2. Now using the same pedal point P, construct the pedal triangle for A2B2C2. This is the green triangle A3B3C 3.

Triangle A1B1C1 is the first pedal triangle, triangle A2B2C2 is the second pedal triangle, and triangle A3B3C 3 is the third pedal triangle for the triangle ABC and the pedal point P.

Theorem

The third pedal triangle is similar to the original triangle.

The proof of our theroem above becomes apparent if we recognize that the point P lies on the circumcircles of all of the triangles AB1C1, A2B1C2, A3B3C2, A2B2C1, and A3B2C3.

For a GSP script that can be used to construct the circumcircle of a triangle please click here.

Geometer's Sketchpad 4.0 users please click here.

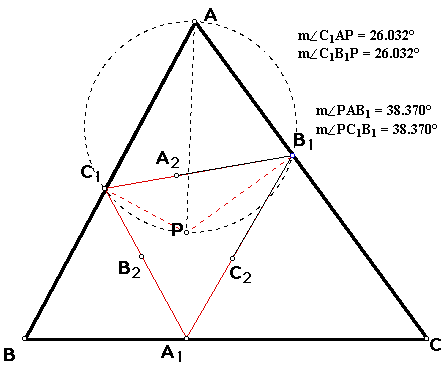
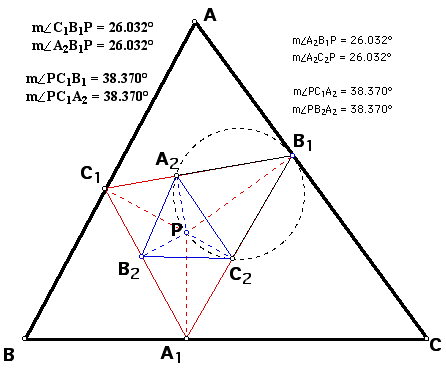
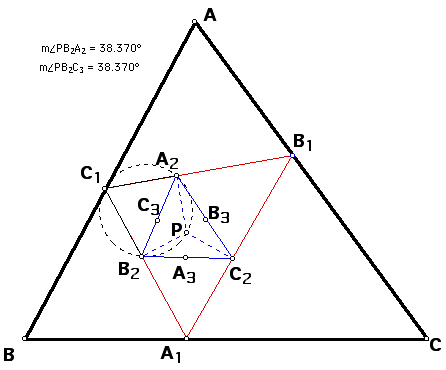
If we strategically join point P to A and likewise point P to other vertices in our triangles below, then we can see

angle C1AP = angle C1B1P = angle A2B1P = angle A2C2P = angle B3C2P = angle B3A3P

and

angle PAB1 = angle PC1B1 = angle PC1A2 = angle PB2A2 = angle PB2C3 = angle PA3C3.

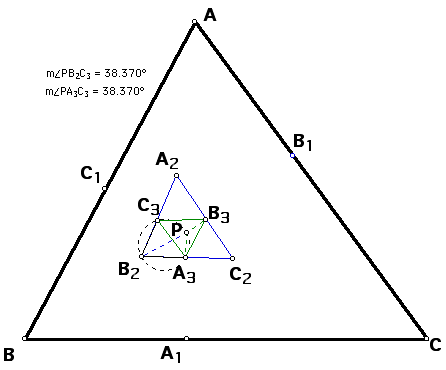
Although the GSP sketch shows that the angles below are equal. No amount of measuring is proof in itself. Each of these angles below that are shown to be equal to each other by measurement, are inscribed in the same circumcircle. They also subtend the same arc of the circumcircle. Therefore, they are congruent angles.

For a GSP sketch of this figure that can be manipulated please click here.

For a GSP sketch of this figure that can be manipulated please click here.

For a GSP sketch of this figure that can be manipulated please click here.

For a GSP sketch of this figure that can be manipulated please click here.

For a GSP sketch of this figure that can be manipulated please click here.

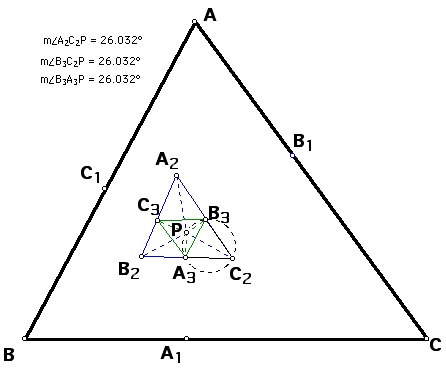
Since angle C1AP = angle B3A3P and angle PAB1 = angle PA3C3

then by angle addition angle A of triangle ABC = angle A3 of triangle A3B3C3.

Likewise it can be shown that angle B = angle B3 and angle C = angle C3.

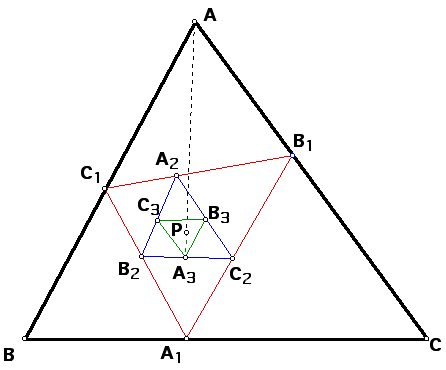
Therefore, by angle, angle similarity, triangle ABC is similar to triangle A3B3C3.

Conjecture: the sixth pedal triangle is similar to the original triangle. Furthermore, any multiple of three pedal triangle is similar to the original triangle.

Conjecture: the n-th pedal n-gon of any n-gon is similar to the original n-gon.

 

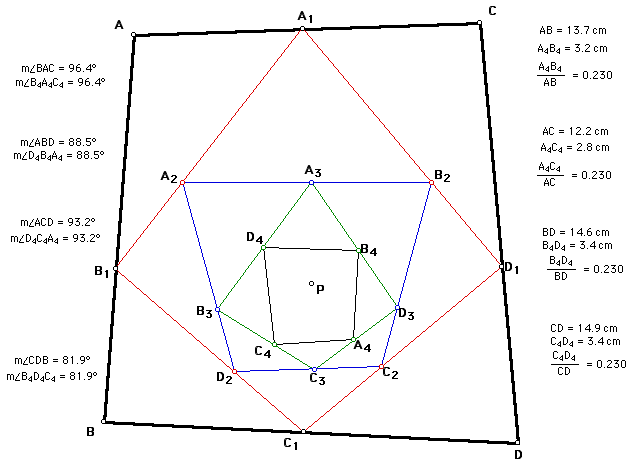These conjectures can be investigated using the Geometer's Sketch Pad.

For a GSP sketch of a quadrilateral and its 4th pedal quadrilateral please click here.

For a GSP script that will construct the 4th pedal quadrilateral for quadrilateral ABCD and pedal point P, please click here.

Geometer's Sketchpad 4.0 users please click here.

Return