
This write-up is for the Final.
EMAT 6680 Final
Project, Fall, 2000
by
Brad Simmons
Part A
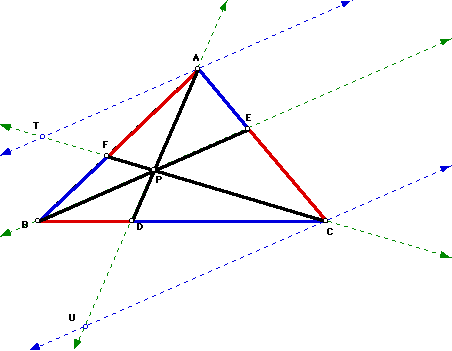
Consider any triangle ABC. We will
select a point P inside the triangle and draw lines AP, BP, and
CP extended to their intersections with the opposite sides in
points D, E, and F respectively.
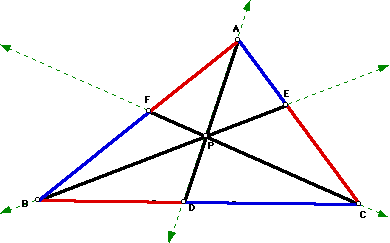 We will now explore the product (AF)(BD)(EC)
and the product (FB)(DC)(EA) for various triangles and various
locations of P.
We will now explore the product (AF)(BD)(EC)
and the product (FB)(DC)(EA) for various triangles and various
locations of P.
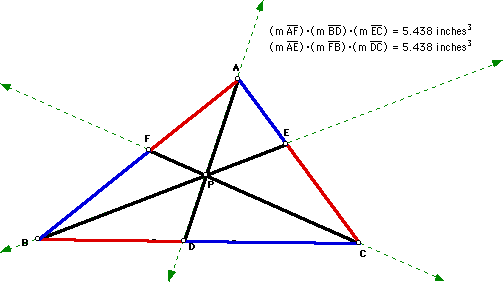 If we measure the segments and do the
calculation of the products to be explored we see that the products
are equal. The image below shows a different triangle with P in
different location.
If we measure the segments and do the
calculation of the products to be explored we see that the products
are equal. The image below shows a different triangle with P in
different location.
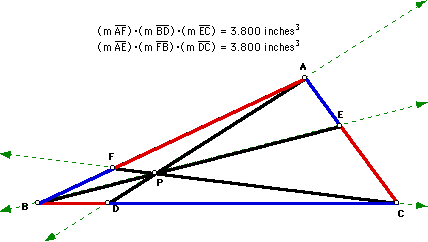 Once again the two products being explored
are equal.
For a dynamic GSP sketch that can be
manipulated please click
here.
Once again the two products being explored
are equal.
For a dynamic GSP sketch that can be
manipulated please click
here.
Part B
If we conjecture that the product of
(AF)(BD)(EC) will always equal the product of (FB)(DC)(EA) in
regard to the conditions stated for triangle ABC in part A, then
we can also conjecture that the ratio of these products is equal
to 1.
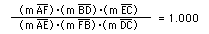 Since no amount of measurement is proof
in itself, we will attempt to prove the ratio shown above is equal
to 1.
Since no amount of measurement is proof
in itself, we will attempt to prove the ratio shown above is equal
to 1.
 Given: triangle
ABC and a point P inside (same conditions in our exploration above),
line UC and line TA are parallel to
line BE.
Prove:
Given: triangle
ABC and a point P inside (same conditions in our exploration above),
line UC and line TA are parallel to
line BE.
Prove: 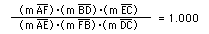 1. triangle AUC is similar to triangle
APE ...( Angle, Angle Similarity)
1. triangle AUC is similar to triangle
APE ...( Angle, Angle Similarity)
- angle CAU is congruent to angle EAP
...(Reflexive Property)
- angle AUC is congruent to angle APE
...(Corresponding angles)
2. AC / AE = UC / PE ...(Corresponding
sides of similar triangles are proportional)
3. Therefore, (AC)(PE) = (AE)(UC)
4. triangle TCA is similar to triangle
PCE ...(Angle, Angle Similarity)
- angle TCA is congruent to angle PCE
...(Reflexive Property)
- angle CTA is congruent to angle CPE
...(Corresponding angles)
5. AC / CE = TA / PE ...(Corresponding
sides of similar triangles are proportional)
6. Therefore, (AC)(PE) = (TA)(CE)
7. triangle FPB is similar to triangle
FTA ...(Angle, Angle Similarity)
- angle BFP is congruent angle AFT
...(Vertical angles)
- angle FBP is congruent to angle FAT
...(Alternate interior angles)
8. BF / AF = BP / TA ...(Corresponding
sides of similar triangles are proportional)
9. Therefore, TA = [(AF)(BP)] / BF
10. triangle DUC is similar to triangle
DPB ...(Angle, Angle Similarity)
- angle CDU is congruent to angle BDP
...(Vertical angles)
- angle UCD is congruent to angle PBD
...(Alternate interior angles)
11. UC / BP = CD / BD ...(Corresponding
sides of similar triangles are proportional)
12. Therefore, UC = [(BP)(CD)] / BD
13. (AE)(UC) = (TA)(CE) ...(Substitution
... step 3 and step 6)
14. (AE)[(BP)(CD)] / BD = (CE)[(AF)(BP)]
/ BF ...(Substitution ... step 13, step 9, and step 12)
15. Hence, (AF)(CE)(BP)(BD) = (BF)(AE)(BP)(CD)
16. Therefore, 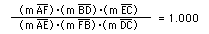
If we construct triangle ABC with lines
rather than segments, then we may be able to generalize our results
from above so that point P can be outside triangle ABC.
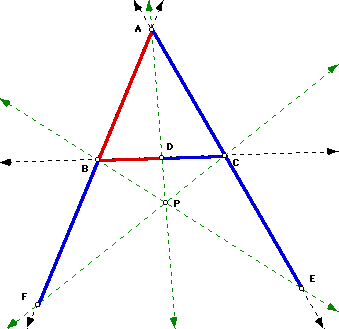 For a dynamic GSP sketch that can be
manipulated please click
here.
For a dynamic GSP sketch that can be
manipulated please click
here.
Part C
Now we will construct triangle DEF.
If point P is inside triangle ABC, then the ratio of the area
of triangle ABC to the area of triangle DEF is always greater
than or equal to 4.
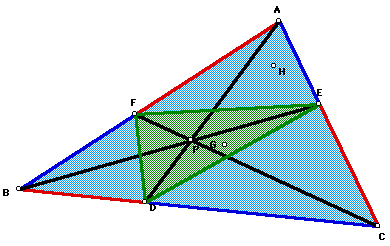 Furthermore, if the point P is at the
centroid (G), then the ratio of the areas will be equal to 4.
For a dynamic GSP sketch that can be
manipulated please click
here.
Furthermore, if the point P is at the
centroid (G), then the ratio of the areas will be equal to 4.
For a dynamic GSP sketch that can be
manipulated please click
here.
Return







