EMAT 6690
Day
3 Equilateral Triangles ... Isosceles Triangles ... Constructions
Equilateral Triangles
An equilateral
triangle is a three sided polygon that
has all three angles that are equal in measure and all three sides
that are congruent. An equilateral triangle is an equiangular triangle
and also a regular triangle.
Each angle of an equilateral triangle
measures 60 degrees.
Click here
for the intermath description for Equilateral Triangles.
Click here
for the intermath description for Equiangular Triangles.
Click here
for the intermath description for Regular Polygons.
Equilateral Triangle Construction
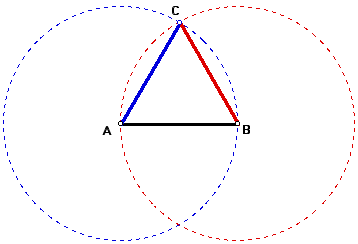Start with segment AB and construct
a circle
with its center at point A and its radius congruent to AB. Now
construct a circle with its center at point B and its radius congruent
to AB. The intersection of the two constructed circles, point
C, is the third vertex of our equilateral triangle.
For a GSP sketch of this equilateral
triangle construction please click
here.
For a GSP script to construct an equilateral
triangle please click
here.
Geometer's Sketchpad 4.0 users please click
here.
Isosceles Triangles
An isosceles
triangle is a triangle with at least two
sides congruent. The congruent sides are called legs. The angles
opposite the legs are base angles. The angle formed by two legs
is the vertex angle. The third side is the base.
If two sides of a triangle are congruent,
then the angles opposite those sides are congruent.
If two angles of a triangle are congruent,
then the sides opposite those angles are congruent.
Click here
for the intermath description for Isosceles Triangles.
Equilateral Triangle Construction
Start with segment AB and a point D located
so angle BAD is an acute angle. Construct a ray AD. Construct
a circle
with its center at point A and its radius congruent to AB. Point
C is the intersection of the constructed circle and ray AD. Segment BC is
the base of the isosceles triangle ABC. Segment AB and AC are
the legs of isosceles triangle ABC.
For a GSP sketch of this isosceles
triangle construction please click
here.
For a GSP script to construct an isosceles
triangle please click
here.
Geometer's Sketchpad 4.0 users please click
here.
Student
Activity
Return