 EMAT 6690
EMAT 6690
Day 4
Right Triangles ... Pythagorean
Theorem ... Trig Ratios ... Constructions
Right Triangles
A right
triangle is a triangle with one right angle.
The side opposite the right angle is called the hypotenuse. The
other two sides are called legs.
In order to construct a right triangle,
begin by constructing two lines perpendicular to each other. The
legs of the triangles will lie on these two perpendicular lines.
The hypotenuse will be the segment connecting the end points (which
do not form the right angle) of the two legs.

Pythagorean Theorem
The pythagorean
theorem states that in a right triangle,
the sum of the squares of the measures of the legs equals the
square of the measure of the hypotenuse.
Click here for the intermath
description of the pythagorean theorem.
Example 1
Find the value of x.
 Solution:
Solution:


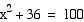

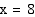
Example 2
Is a triangle having sides measuring
18, 34, and 39 a right triangle?
Solution:
In a right triangle
the hypotenuse will always be the longest side and the legs will
always be the two shorter sides. Therefore, we can label our right
triangle as it is shown below.
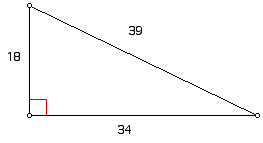 Now use the pythagorean theorem to
test if this is a right triangle.
Now use the pythagorean theorem to
test if this is a right triangle.

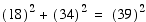
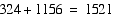
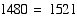 Since the pythagorean theorem yields
a false statement, then this triangle with sides measuring 18, 34, and
39 is not a right triangle.
Since the pythagorean theorem yields
a false statement, then this triangle with sides measuring 18, 34, and
39 is not a right triangle.
Trigonometric Ratios
Trigonometry means
triangle measurement. A ratio of the lengths of two sides of a
right triangle is called a trigonometric
ratio. The three most common
ratios are sine, cosine, and tangent.

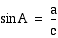
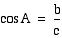
 Trionometric ratios
are related to the acute angles of a right triangle, not the right
angle. The value of a trigonometric ratio depends only on the
measure of the angle and not on the size of the triangle. The
ratios for the sine of angle A, the cosine of angle A, and the
tangent of angle A are shown above.
The sine of angle
A is equal to the opposite side (side a) divided by the
hypotenuse (side c).
The cosine of angle
A is equal to the adjacent side (side b) divided by the
hypotenuse (side c).
The tangent of angle
A is equal to the opposite side divided by the
adjacent side.
To solve problems using
trigonometric ratios, a calculator or a trigonometric table must
be used to find the value of the trigonometic ratio. For example
the sin of a 40 degree angle is .6428 rounded to four decimal
places.
Trionometric ratios
are related to the acute angles of a right triangle, not the right
angle. The value of a trigonometric ratio depends only on the
measure of the angle and not on the size of the triangle. The
ratios for the sine of angle A, the cosine of angle A, and the
tangent of angle A are shown above.
The sine of angle
A is equal to the opposite side (side a) divided by the
hypotenuse (side c).
The cosine of angle
A is equal to the adjacent side (side b) divided by the
hypotenuse (side c).
The tangent of angle
A is equal to the opposite side divided by the
adjacent side.
To solve problems using
trigonometric ratios, a calculator or a trigonometric table must
be used to find the value of the trigonometic ratio. For example
the sin of a 40 degree angle is .6428 rounded to four decimal
places.
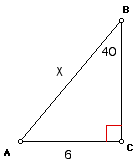
Example:
Find the value for x.
 Solution:
Solution:


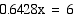
 (the value of x has been rounded
to four decimal places)
(the value of x has been rounded
to four decimal places)
Student
Activity
Return






