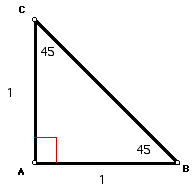EMAT 6690
EMAT 6690
Day 5
Special Right Triangles ... 30,
60, 90 ... 45, 45, 90 ... Constructions
30, 60, 90 Right Triangles
Construction
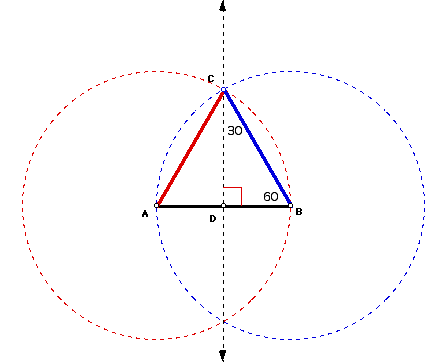 To construct a 30,
60, 90 triangle start with segment AB. Now construct an equilateral
triangle ABC by constructing circle A with a radius congruent to AB and
circle B also with a radius of AB. The intersection of these
two circles, point C, is the third vertex of the constructed equilateral
triangle. Now construct a line perpendicular to segment AB that
passes through point C. Triangle CDB is a 30, 60, 90 triangle.
For a GSP sketch of
the 30, 60, 90 triangle construction please click
here.
For a GSP script to
construct a 30, 60, 90 triangle please click
here.
Geometer's Sketchpad
4.0 users please click
here.
To construct a 30,
60, 90 triangle start with segment AB. Now construct an equilateral
triangle ABC by constructing circle A with a radius congruent to AB and
circle B also with a radius of AB. The intersection of these
two circles, point C, is the third vertex of the constructed equilateral
triangle. Now construct a line perpendicular to segment AB that
passes through point C. Triangle CDB is a 30, 60, 90 triangle.
For a GSP sketch of
the 30, 60, 90 triangle construction please click
here.
For a GSP script to
construct a 30, 60, 90 triangle please click
here.
Geometer's Sketchpad
4.0 users please click
here.
Consider triangle ABC
shown below.
 The hypotenuse is twice
as long as the shorter leg and the longer leg is the square root
of 3 times longer than the shorter leg.
The hypotenuse is twice
as long as the shorter leg and the longer leg is the square root
of 3 times longer than the shorter leg.
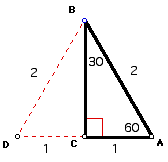 Since point C is the
midpoint of segment AD, it is easy to see that the hypotenuse
AB of the 30, 60, 90 triangle ABC is twice as long as the shorter
leg AC. By using the pythagorean theorem we can show the longer
leg is the square root of 3 times longer than the shorter leg.
Since point C is the
midpoint of segment AD, it is easy to see that the hypotenuse
AB of the 30, 60, 90 triangle ABC is twice as long as the shorter
leg AC. By using the pythagorean theorem we can show the longer
leg is the square root of 3 times longer than the shorter leg.
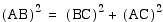
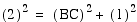
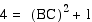
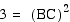
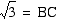
45, 45, 90 Triangles
Construction
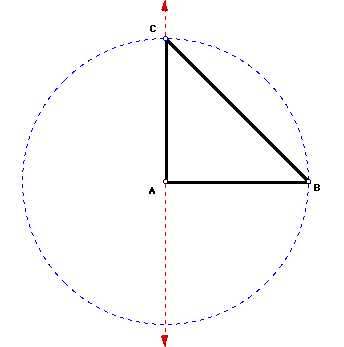 To construct a 45, 45, 90 triangle
start with segment AB. Construct a line perpendicular to AB passing
through point A. Now construct circle A with its center at point
A and its radius congruent to segment AB. The intersection of
the constructed perpendicular line and constructed circle is point
C. Point C is the third vertex of the constructed 45, 45, 90 triangle
ABC.
For a GSP sketch of
the 45, 45, 90 triangle construction please click
here.
For a GSP script to
construct a 45, 45, 90 triangle please click
here.
Geometer's Sketchpad
4.0 users please click
here.
To construct a 45, 45, 90 triangle
start with segment AB. Construct a line perpendicular to AB passing
through point A. Now construct circle A with its center at point
A and its radius congruent to segment AB. The intersection of
the constructed perpendicular line and constructed circle is point
C. Point C is the third vertex of the constructed 45, 45, 90 triangle
ABC.
For a GSP sketch of
the 45, 45, 90 triangle construction please click
here.
For a GSP script to
construct a 45, 45, 90 triangle please click
here.
Geometer's Sketchpad
4.0 users please click
here.
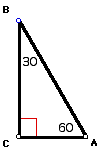
Now consider triangle
ABC shown below.
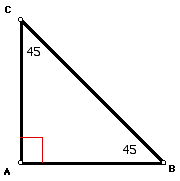 In a 45, 45, 90 triangle,
the two legs have equal measures and the hypotenuse is the square
root of 2 times as long as a leg.
In a 45, 45, 90 triangle,
the two legs have equal measures and the hypotenuse is the square
root of 2 times as long as a leg.
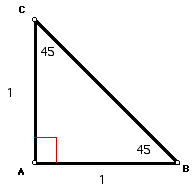 Once again we can use
the pythagorean theorem to show the length of the hypotenuse BC.
Once again we can use
the pythagorean theorem to show the length of the hypotenuse BC.
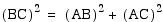
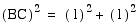
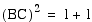
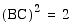
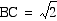
Student
Activity
Return