EMAT 6690
~Circumcenter~Orthocenter~
~Euler
Line ~
A perpendicular bisector is
a line that bisects and is perpendicular to the side of a triangle.
The point of concurrency of the perpendicular bisectors is called
the circumcenter of a triangle.
An investigation than can be used as a teaching tool
for the circumcenter.
Investigation
- Step 1
On a sheet of paper or wax paper, draw
a large scalene acute triangle. Make the triangle as large
as you can.
- Step 2
Take the acute triangle that you constructed and label it ABD,
as shown below.
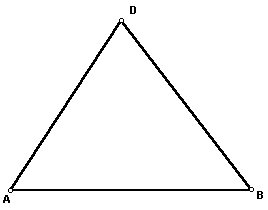
- Step 3
Construct the three perpendicular bisectors. Find the midpoints
of the three sides of the triangle, and label midpoints E,
F, and J. Label the circumcenter C.
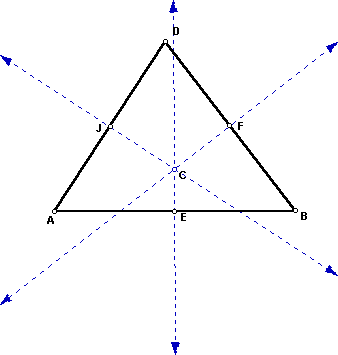
- Step 4
Use your compass to answer the following questions: Is
the circumcenter the same distance from the vertices? From
the three sides? Take a look at how the circumcenter divides
each perpendicular bisectors. Is the circumcenter the midpoint
of each perpendicular bisector?
- Step 5
The circumcenter is the same distance from the vertices, but
it is not the same distance from the three sides. The circumcenter
is not the midpoint of each perpendicular bisector.
An altitude is a perpendicular
line drawn from a vertex of a triangle to the opposite side.
The point of concurrency of the altitudes is called the orthocenter
of a triangle.
An investigation than can be used as a teaching tool
for the circumcenter.
Investigation
- Step 1
On a sheet of paper or wax paper, draw
a large scalene acute triangle. Make the triangle as large
as you can.
- Step 2
Take the acute triangle that you constructed and label it ABD,
as shown below.
- Step 3
Construct the three altitudes, and label the altitudes AE,
BF, and DJ. Label the orthocenter H.
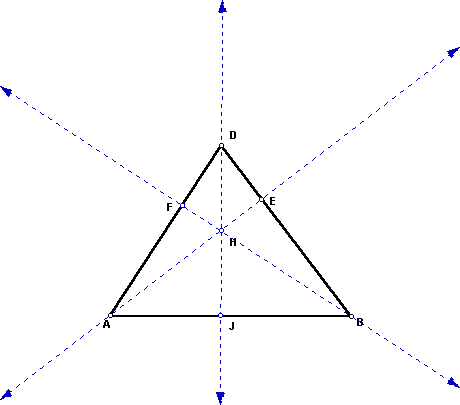
- Step 4
Use your compass to answer the following questions: Is
the orthocenter the same distance from the vertices? From
the three sides? Take a look at how the orthocenter divides
each perpendicular bisectors. Is the orthocenter the midpoint
of each perpendicular bisector?
- Step 5
The orthocenter is not the same distance from the vertices and
the three sides. The orthocenter is not the midpoint of
each perpendicular bisector.
The Euler Line is always contains
three of the four points of concurrency. THe Euler Line
is named after Swiss mathematician Leonhard Euler, who proved
that the three points of concurrency were collinear.
An investigation that can be used as a teaching tool
for the Euler Line.
Investigation
- Step 1
On a sheet of paper or wax paper, draw
a large scalene acute triangle. Make the triangle as large
as you can.
- Step 2
Take the acute triangle and label it ABD, as shown below.
- Step 3 Now construct the four points of
concurrency on your triangle. Label the centroid G,
the incenter I, the circumcenter C, and the orthocenter
H.
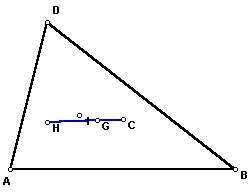Students should be able to complete
the following conjecture at this point.
The -(centroid)-,-(circumcenter)-, and the -(orthocenter)- are the three points of concurrency
that always lie on the Euler line.
- Step 4
With a compass, compare lengths of the
two parts on the Euler segment.
Students should be able to complete
the following conjecture at this point.
The -(centroid)-
divides the Euler segment into two parts so that the smaller part
is -(half as long as)- the larger part.
Student Activity
Return