The nine point circle is located inside of the triangle. It passes through the three midpoints of the sides, the three feet of the altitudes, and the three midpoints of the segments from the respective vertices to the orthocenter.

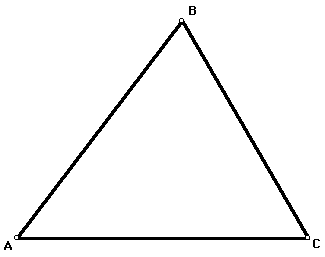
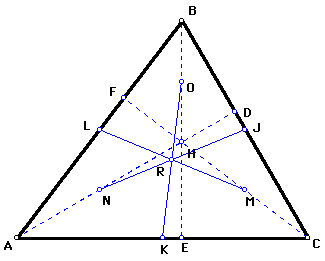
• Step 1    Construct a large scalene triangle. Label it ABC.

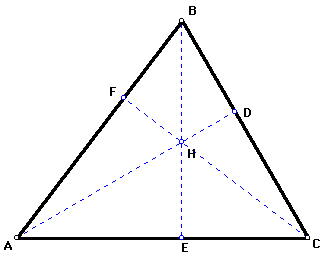
• Step 2    Construct the altitude to each side of the triangle and label the points of intersection with the sides D, E, and F. Label the orthocenter H.

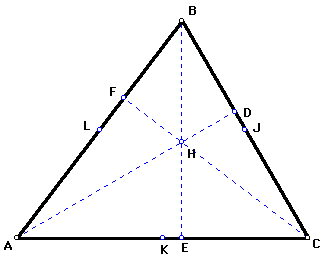
• Step 3    Construct the midpoints of each side of the triangle. Label the points J, K, and L so that J is the midpoint of BC and K is the midpoint of AC.

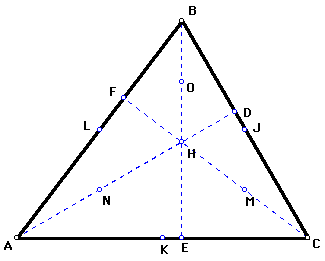
• Step 4     Construct the midpoints of AH, BH, and CH and label the points MNO so that M is the midpoint of CH, N is the midpoint of AH, and O is the midpoint of BH.

• Step 5    Construct the line segments connecting point K to O, point J to N, and point L to M. They should all intersect in one point. Label that point R.

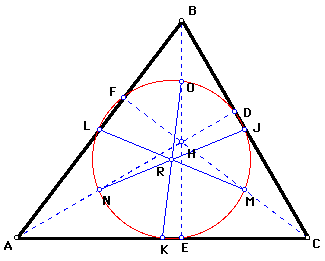
• Step 6    Construct a circle with radius RK and center at R. It should pass through all nine points: D, E, F, J, K, L, M, N, and O.

Student Activity