

EMAT 6700
by Brad Simmons
Transformations and Reflections
Use geometer's sketchpad investigate transformations and reflections.
Transformations
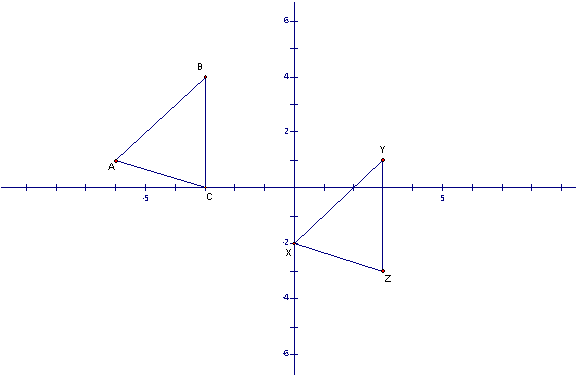
The figure above shows how triangle ABC is mapped to triangle XYZ.
Each point of triangle ABC with coordinates ( x, y ) is mapped to triangle XYZ with coordinates ( x+6, y-3).
Please click here for a geometer's sketchpad sketch of the figure shown above.
Use geometer's sketchpad to draw the transformation image described below.
1. Map triangle ABC (shown above) with coordinates ( x, y ) to triangle XYZ with coordinates ( x-4, y ).
2. Map triangle ABC (shown above) with coordinates ( x, y ) to triangle XYZ with coordinates ( x+8, y+7 ).
3. Map triangle ABC (shown above) with coordinates ( x, y ) to triangle XYZ with coordinates ( -x, -y ).
Reflections
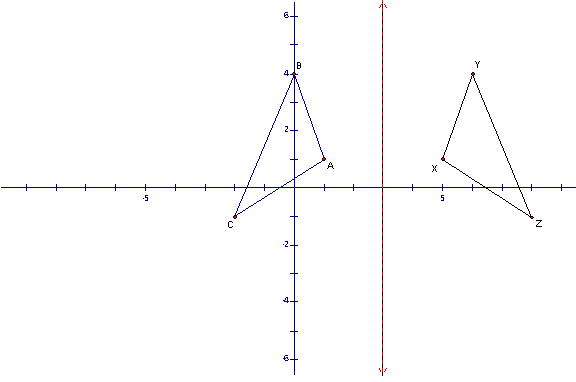
The figure shown above shows how triangle ABC is mapped onto triangle XYZ. The transformation is each point of triangle ABC with coordinates ( x, y ) is mapped to triangle XYZ with coordinates ( -x+6, y ). The triangle XYZ is the reflected image of triangle ABC with respect to the red vertical line with an equation of x = 3.
Please click here for a geometer's sketchpad sketch of the figure shown above.
Use geometer's sketchpad to draw the reflected image described below. The reflection is with respect to what line?
1. Map triangle ABC (shown above) with coordinates ( x, y ) to triangle XYZ with coordinates ( -x-4, y ).
2. Map triangle ABC (shown above) with coordinates ( x, y ) to triangle XYZ with coordinates ( x, -y+8 ).