

EMAT 6700
by Brad Simmons
Golden Rectangles
Use geometer's sketchpad construct golden rectangles.
1. Construct square ABCD.
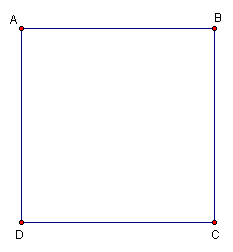
2. Construct the midpoint of segment AB. Label the midpoint M.
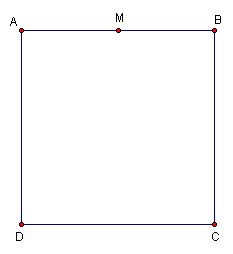
3. Construct line AB. Construct segment MC. Select point M and segment MC. Construct circle by center and radius. Construct the intersection of circle M and line AB. Label the point of intersection P.
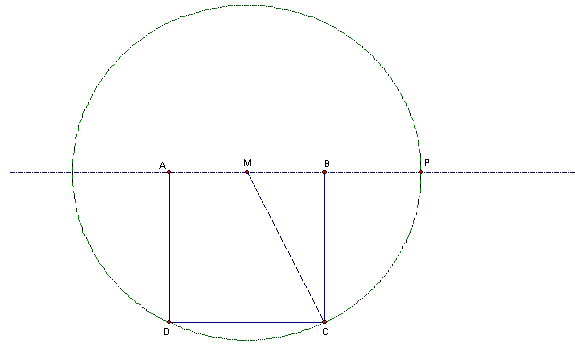
4. Select circle M and segment MC. Hide the objects. Construct a line through point P that is perpendicular to segment AB. Construct line DC. Construct the intersection of line DC and the perpendicular line. Label the point of intersection point Q.
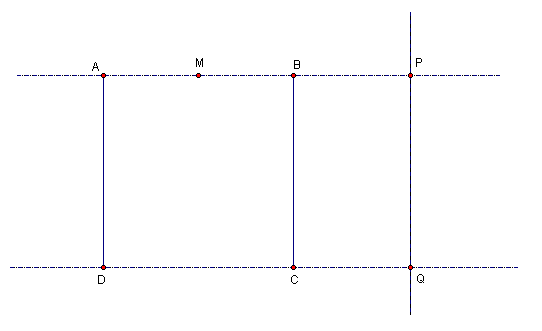
5. Rectangle APQD is a golden rectangle because the ratio of its length to its width is 1.618 (or 1.62 rounded to the nearest hundredth). Rectangles whose sides have this ratio are said to be the most pleasing to the human eye.
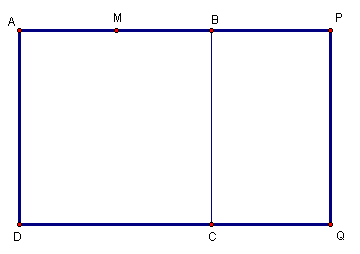
Check the golden ratio by finding the value of AP/QP.
Please click here for a geometer's sketchpad sketch of the figure shown above.
Golden Spiral
A figure consisting of similar golden rectangles is shown below.
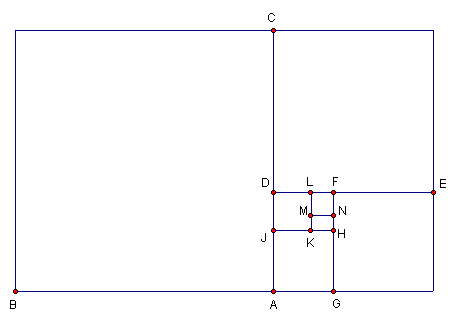
Please click here for a geometer's sketchpad sketch of the figure shown above.
Use the instructions below to draw quarter-circle arcs that form a spiral like that found in the shell of a chambered nautilus. The chambered nautilus can be found in the South Pacific and Indian Oceans.
1. Using A as a center, draw an arc that passes through point B and point C.
2. Using D as a center, draw an arc that passes through point C and point E.
3. Using F as a center, draw an arc that passes through point E and point G.
4. Using H as a center, draw an arc that passes through point G and point J.
5. Using K as a center, draw an arc that passes through point J and point L.
6. Using M as a center, draw an arc that passes through point L and point N.
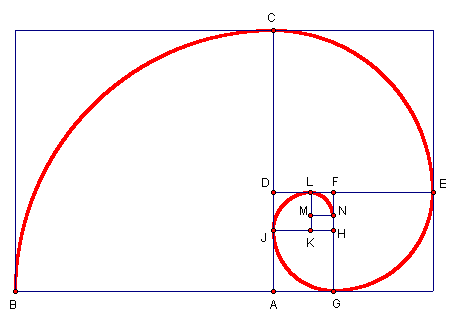
Please click here for a geometer's sketchpad sketch of the figure shown above.