EMAT 6700

by Brad Simmons

Four Color Problem

Use geometer's sketchpad to investigate the four color problem.

Mapmakers have long believed that only four colors are needed to distinguish among any number of countries on a plane map.  This conjecture eventually attracted the attention of mathematicians and became known as "the four color problem."  Finally, in the 1980's with the help of computers a proof was accomplished confirming the four color conjecture.  The problems below attempt to show some to the complexities associated with the four color problem.

Assume that each closed region is a different country on a map.  Countries that meet only in one point may have the same color provided they do not share a common border (borders are line segments).  Countries that have a common border must have a different color.

What is the minimum number of colors necessary for each map?

                                     1.

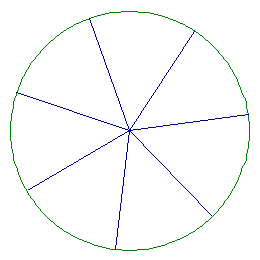
Please click here for a geometer's sketchpad sketch of the solution for the figure above.

                                     2.

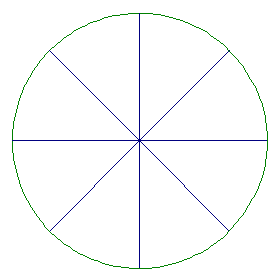
Please click here for a geometer's sketchpad sketch of the figure above.

                                       3.

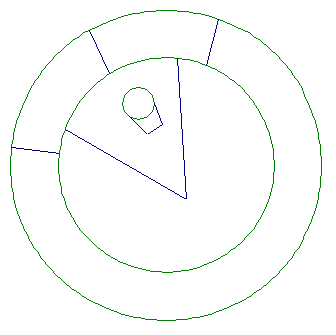
Please click here for a geometer's sketchpad sketch of the figure above.

                                      4.

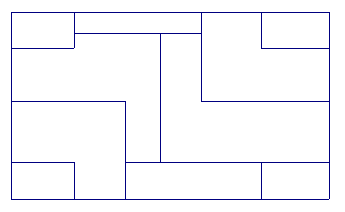
Please click here for a geometer's sketchpad sketch of the figure above.

                                   5.

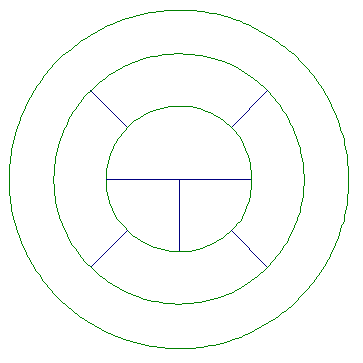
Please click here for a geometer's sketchpad sketch of the figure above.

Draw some plane maps other than the problems shown above.  Show how each can be colored using four colors.  Can the map be colored with less than four colors?

Return