---

FINAL

Complete a Write-up on your Web Page for the following investigation. This should be individual work.

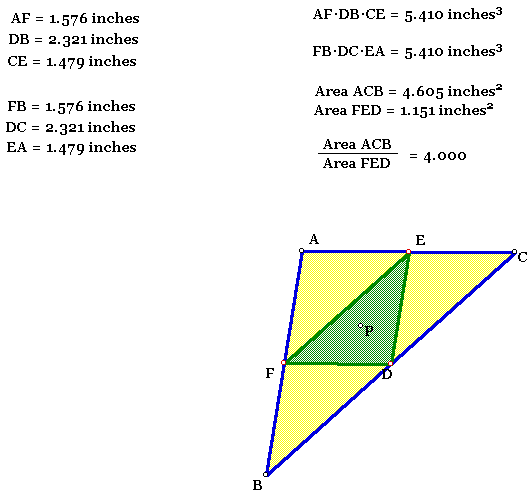
A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

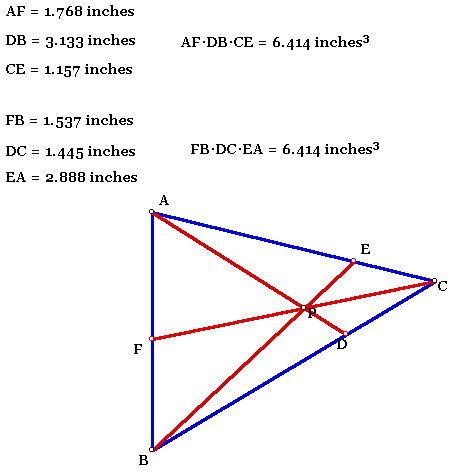
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P. For a GSP illustration click here.

B. Conjecture? Prove it! (you may need draw some parallel lines to produce some similar triangles) Also, it probably helps to consider the ratio (completed with the aid of the ever most talented and learned colleague Ms. Amy Hackenberg).

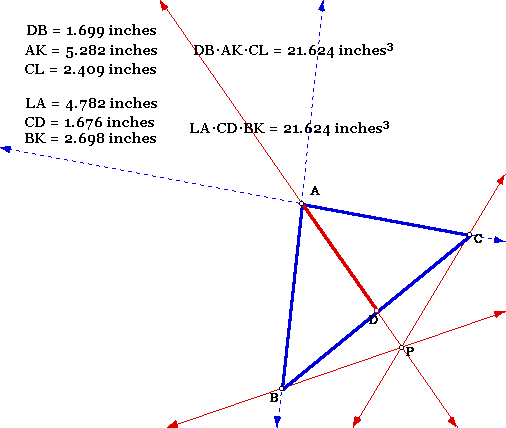
Triangle BPD and BLC are similar since they share a common angle and DP is parallel to CN. Therefore, the ratios of BD/BC=DP/CL. Likewise triangle CPD and CKB are similar, angle C is shared and DP is parallel to BK. Therefore the ratios of CD/BC=DP/BK; and then (BD)(CL)=(BC)(DP)=(CD)(BK)=(BC)(DP).

Triangle BFK and AFP are similar with AAA, since angle BFK and AFK are vertical angles and BK is parallel to AP, this gives angle BAP=angle KBA from alternate interior angles; likewise for the other two angles. Since similar, then the following ratios are true: BF/AF=BK/AP then BK= (BF)(AP)/(AF).

Likewise triangles AEP and LEC are similar with AAA with the same reasoning as above. Then CL/AP=CE/AE so CL =(AP)(CE)/(AE).

Using substitution of BK and CL yields (BD) ((AP)(CE)/AE)=(CD)((BF)(AP)/AF); and canceling AP from both sides yield the desired results of (AF)(BD)(CE)=(BF)(CD)(AE).

QED

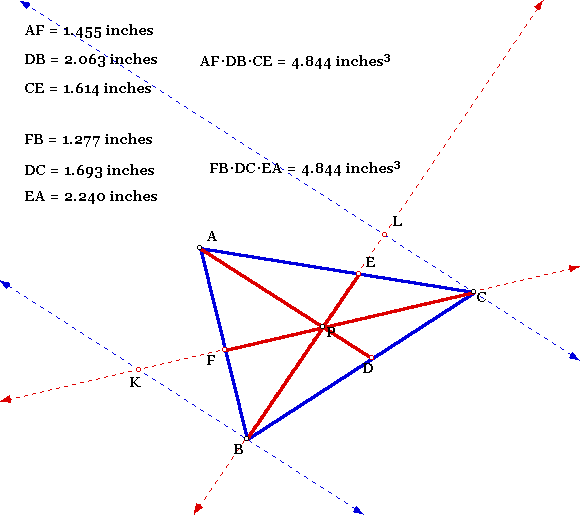
Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle? Show a working GSP sketch.

For GSP sketch click here.

C. Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. For GSP sketch to illustrate click here; however, this is not a proof. When is it equal to 4? The ratio is equal to 4 when point P is the centroid.