

In this write-up, I investigate the graphs of the polar equations r = a + bcos(kq) and r = a + bsin(kq), where a, b, and k are natural numbers (except in the special case when a = 0). First, I discuss the equation r = a + bcos(kq) as k changes when a = b, a < b, a > b, and a = 0. Then I discuss the equation r = a + bsin(kq) as k changes when a = b, a < b, a > b, and a = 0.
The following example contains the graphs r = 1 + 1cos(1q), r = 2 + 2cos(1q), and r = 3 + 3cos(1q).
Note that the graph of an equation of the form r = a + bcosq is called a limaçon in trigonometry. In the case when a = b, the graph is a special limaçon called a cardioid (because it is heart-shaped).
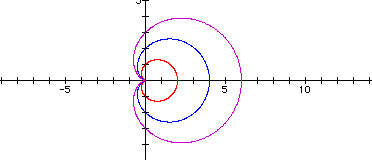
The following example contains the graphs r = 1 + 1cos(2q), r = 2 + 2cos(2q), and r = 3 + 3cos(2q).
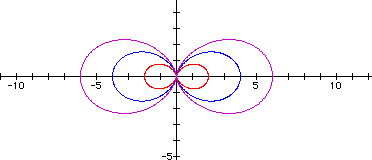
The following example contains the graphs r = 1 + 1cos(3q), r = 2 + 2cos(3q), and r = 3 + 3cos(3q).
Click here to see a movie of the equation r = 2 + 2cos(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
The first conjecture I can make is that each graph has "k" loops to it, and that each loop seems to be congruent. But no matter how many loops the graph contains, the entire curve seems to be symmetric about the x-axis.
I also notice that each graph has a loop that lies on the positive x-axis, and that the graph seems to cross the positive x-axis at a distance that is 2a (or 2b) from the origin. This is because the positive x-axis has an angle measure of 0 degrees, and since the cosine of 0 degrees is 1, the equations reduce to r = a + b. Since a and b are equal in this case, then r = 2a = 2b.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
I note, too, that each graph passes through the origin. This occurs whenever kq = 180 degrees, because the cosine of 180 degrees is -1. Therefore, the equations reduce to r = a + (-b), and since a = b, it follows that r = 0.
Finally, I would like to point out that since the cosine of an angle is always between -1 and 1 (inclusive), and because a = b in this case, r must always be positive or zero. The value of r, then, can be at the least 0 and at the most 2a (or 2b).
The following example contains the graphs r = 1 + 2cos(1q), r = 2 + 3cos(1q), and r = 3 + 4cos(1q).
Note that the graph of an equation of the form r = a + bcosq is called a limaçon in trigonometry. In the case when a < b, the graph is a special limaçon with an extra loop.
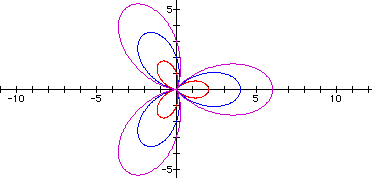
The following example contains the graphs r = 1 + 2cos(2q), r = 2 + 3cos(2q), and r = 3 + 4cos(2q).
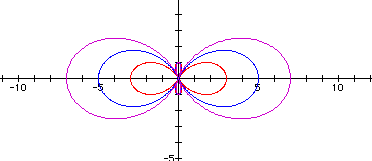
The following example contains the graphs r = 1 + 2cos(3q), r = 2 + 3cos(3q), and r = 3 + 4cos(3q).

Click here to see a movie of the equation r = 1 + 2cos(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
The first conjecture I can make is that each graph has "k" loops to it, and that each loop seems to be congruent. But no matter how many loops the graph contains, the entire curve seems to be symmetric about the x-axis.
I also notice that each graph has a loop that lies on the positive x-axis, and that the graph seems to cross the positive x-axis at a distance that is a + b from the origin. This is because the positive x-axis has an angle measure of 0 degrees, and since the cosine of 0 degrees is 1, the equations reduce to r = a + b.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
Finally, I would like to point out that each graph resembles the corresponding graphs of the form r = a + bcos(kq) when a = b, but that these new graphs have extra loops. This is why: the cosine of an angle is always between -1 and 1 (inclusive). The value of r, then, can be at the least a + (-b) and at the most a + b. Since a < b, it follows that r can be positive, negative, or 0. When r = 0, the graph crosses through the origin, and when r is negative, the extra loops occur.
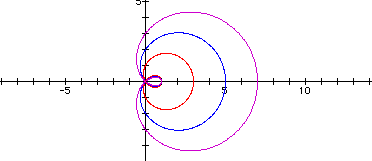
The following example contains the graphs r = 2 + 1cos(1q), r = 3 + 2cos(1q), and r = 4 + 3cos(1q).
Note that the graph of an equation of the form r = a + bcosq is called a limaçon in trigonometry. In the case when a > b, the graph is a special limaçon with no extra loop.

The following example contains the graphs r = 2 + 1cos(2q), r = 3 + 2cos(2q), and r = 4 + 3cos(2q).
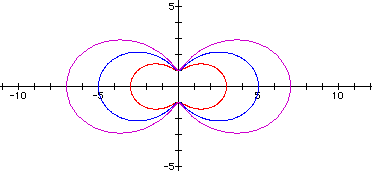
The following example contains the graphs r = 2 + 1cos(3q), r = 3 + 2cos(3q), and r = 4 + 3cos(3q).
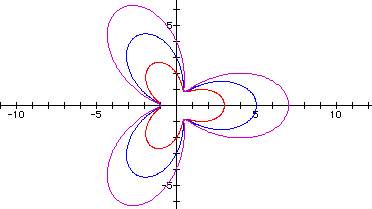
Click here to see a movie of the equation r = 2 + 1cos(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
The first conjecture I can make is that each graph has "k" loops to it, and that each loop seems to be congruent. But no matter how many loops the graph contains, the entire curve seems to be symmetric about the x-axis.
I also notice that each graph has a loop that lies on the positive x-axis, and that the graph seems to cross the positive x-axis at a distance that is a + b from the origin. This is because the positive x-axis has an angle measure of 0 degrees, and since the cosine of 0 degrees is 1, the equations reduce to r = a + b.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
Finally, I would like to point out that each graph resembles the corresponding graphs of the form r = a + bcos(kq) when a = b, but that these new graphs do not pass through the origin. This is why: the cosine of an angle is always between -1 and 1 (inclusive). The value of r, then, can be at the least a + (-b) and at the most a + b. Since a > b, it follows that r must always be positive, and so the graph can never pass through the origin.
The following example contains the graphs r = 1cos(1q), r = 2cos(1q), and r = 3cos(1q).
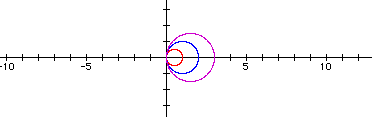
The following example contains the graphs r = 1cos(2q), r = 2cos(2q), and r = 3cos(2q).
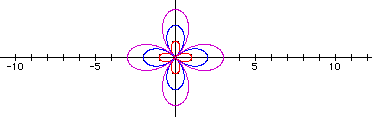
The following example contains the graphs r = 1cos(3q), r = 2cos(3q), and r = 3cos(3q).

Click here to see a movie of the equation r = 2cos(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
Note that the graph of an equation of the form r = bcos(kq) is called a rose in trigonometry.
The first conjecture I can make is that when k is odd, the rose has k leaves, and when k is even, the rose has 2k leaves; either way, each leaf seems to be congruent. And, no matter how many leaves the graph contains, the entire curve seems to be symmetric about the x-axis.
I also notice that each graph has a leaf that lies on the positive x-axis, and that the graph seems to cross the positive x-axis at a distance that is "b" from the origin. This is because the positive x-axis has an angle measure of 0 degrees, and since the cosine of 0 degrees is 1, the equations reduce to r = b.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
I note, too, that each graph passes through the origin. This occurs whenever kq = 90 and 270 degrees, because the cosine of 90 and 270 degrees is 0. Therefore, it follows that r = 0 in these cases.
Finally, I would like to point out that since the cosine of an angle is always between -1 and 1 (inclusive), r can be positive, negative, or zero. The value of r, then, can be at the least -b and at the most b.
The following example contains the graphs r = 1 + 1sin(1q), r = 2 + 2sin(1q), and r = 3 + 3sin(1q).
Note that the graph of an equation of the form r = a + bsinq is called a limaçon in trigonometry. In the case when a = b, the graph is a special limaçon called a cardioid (because it is heart-shaped).
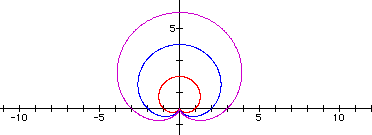
The following example contains the graphs r = 1 + 1sin(2q), r = 2 + 2sin(2q), and r = 3 + 3sin(2q).

The following example contains the graphs r = 1 + 1sin(3q), r = 2 + 2sin(3q), and r = 3 + 3sin(3q).
Click here to see a movie of the equation r = 2 + 2sin(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
The first conjecture I can make is that each graph has "k" loops to it, and that each loop seems to be congruent.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
I note, too, that each graph passes through the origin. This occurs whenever kq = 270 degrees, because the sine of 270 degrees is -1. Therefore, the equations reduce to r = a + (-b), and since a = b, it follows that r = 0.
Finally, I would like to point out that since the sine of an angle is always between -1 and 1 (inclusive), and because a = b in this case, r must always be positive or zero. The value of r, then, can be at the least 0 and at the most 2a (or 2b).
The following example contains the graphs r = 1 + 2sin(1q), r = 2 + 3sin(1q), and r = 3 + 4sin(1q).
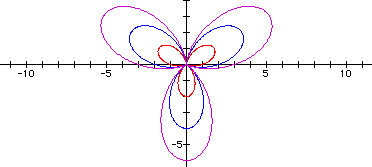
Note that the graph of an equation of the form r = a + bsinq is called a limaçon in trigonometry. In the case when a < b, the graph is a special limaçon with an exta loop.
The following example contains the graphs r = 1 + 2sin(2q), r = 2 + 3sin(2q), and r = 3 + 4sin(2q).

The following example contains the graphs r = 1 + 2sin(3q), r = 2 + 3sin(3q), and r = 3 + 4sin(3q).
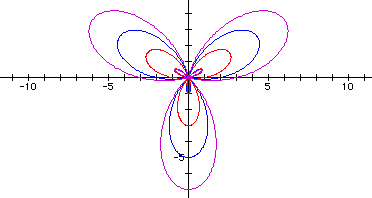
Click here to see a movie of the equation r = 1 + 2sin(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
The first conjecture I can make is that each graph has "k" loops to it, and that each loop seems to be congruent.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
Finally, I would like to point out that each graph resembles the corresponding graphs of the form r = a + bsin(kq) when a = b, but that these new graphs have extra loops. This is why: the sine of an angle is always between -1 and 1 (inclusive). The value of r, then, can be at the least a + (-b) and at the most a + b. Since a < b, it follows that r can be positive, negative, or 0. When r = 0, the graph crosses through the origin, and when r is negative, the extra loops occur.
The following example contains the graphs r = 2 + 1sin(1q), r = 3 + 2sin(1q), and r = 4 + 3sin(1q).
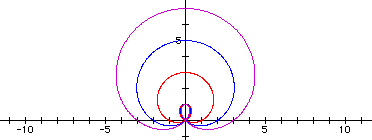
Note that the graph of an equation of the form r = a + bsinq is called a limaçon in trigonometry. In the case when a > b, the graph is a special limaçon with no extra loop.

The following example contains the graphs r = 2 + 1sin(2q), r = 3 + 2sin(2q), and r = 4 + 3sin(2q).
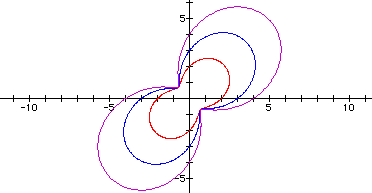
The following example contains the graphs r = 2 + 1sin(3q), r = 3 + 2sin(3q), and r = 4 + 3sin(3q).

Click here to see a movie of the equation r = 2 + 1sin(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
The first conjecture I can make is that each graph has "k" loops to it, and that each loop seems to be congruent.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
Finally, I would like to point out that each graph resembles the corresponding graphs of the form r = a + bcos(kq) when a = b, but that these new graphs do not pass through the origin. This is why: the sine of an angle is always between -1 and 1 (inclusive). The value of r, then, can be at the least a + (-b) and at the most a + b. Since a > b, it follows that r must always be positive, and so the graph can never pass through the origin.
The following example contains the graphs r = 1sin(1q), r = 2sin(1q), and r = 3sin(1q).
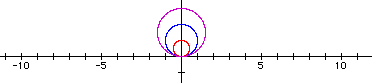
The following example contains the graphs r = 1sin(2q), r = 2sin(2q), and r = 3sin(2q).

The following example contains the graphs r = 1sin(3q), r = 2sin(3q), and r = 3sin(3q).
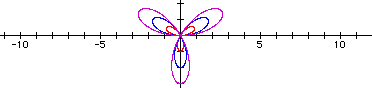
Click here to see a movie of the equation r = 2sin(kq), as k varies from 0 to 10 and back.
My conjectures, based on the example graphs:
Note that the graph of an equation of the form r = bsin(kq) is called a rose in trigonometry.
The first conjecture I can make is that when k is odd, the rose has k leaves, and when k is even, the rose has 2k leaves; either way, each leaf seems to be congruent. And, no matter how many leaves the graph contains, the entire curve seems to be symmetric about the y-axis.
Next, I conjecture that as "a" and "b" get larger, the graph gets larger.
I note, too, that each graph passes through the origin. This occurs whenever kq = 0 and 180 degrees, because the sine of 0 and 180 degrees is 0. Therefore, it follows that r = 0 in these cases.
Finally, I would like to point out that since the sine of an angle is always between -1 and 1 (inclusive), r can be positive, negative, or zero. The value of r, then, can be at the least -b and at the most b.