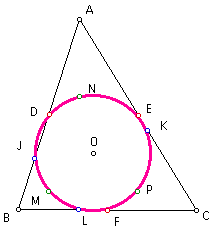
Given triangle ABC. Let point D be the midpoint of side AB, point E be the midpoint of side AC, and point F be the midpoint of side BC (Note triangle DEF is the medial triangle).
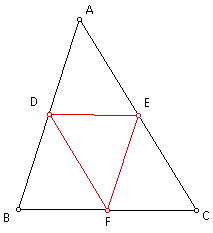
Let point J be the foot of the altitude from point C to side AB, point K be the foot of the altitude from point B to side AC, and point L be the foot of the altitude from point A to side BC (Note triangle JKL is the orthic triangle).
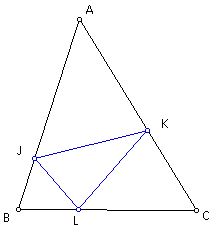
And if point H is the orthocenter of triangle ABC, let point M be the midpoint of HB, point N be the midpoint of HA, and point P be the midpoint of HC (Note triangle MNP is the orthocenter mid-segment triangle).
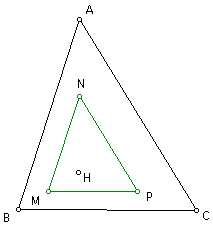
Prove points D, E, F, J, K, L, M, N, and P lie on a common circle (called the nine-point circle).
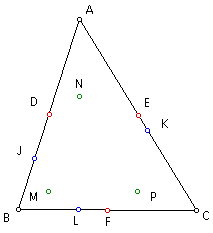
In triangle ABC, since D and E are midpoints of sides AB and AC (by construction), then segment DE is parallel to side BC.
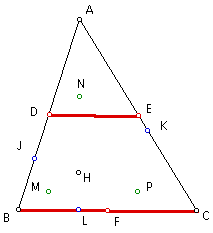
In triangle BCH, since M and P are midpoints of sides BH and HC (by construction), then segment MP is parallel to side BC.
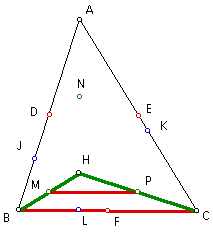
Since segment DE is parallel to side BC, and segment MP is parallel to side BC, then segments DE and MP are parallel to each other.
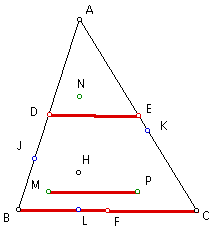
In triangle BAH, since M and D are midpoints of sides BH and BA (by construction), then segment MD is parallel to side HA.
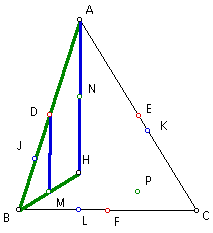
In triangle CAH, since E and P are midpoints of sides AC and HC (by construction), then segment EP is parallel to side HA.
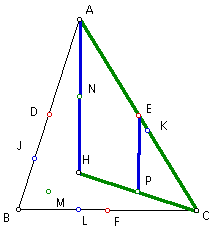
Since segment MD is parallel to side HA, and segment EP is parallel to side HA, then segments MD and EP are parallel to each other.
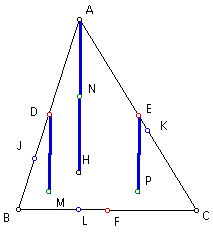
Since segment MD is parallel to segment HA, and segment HA lies on segment AL, then segment MD is parallel to segment AL.
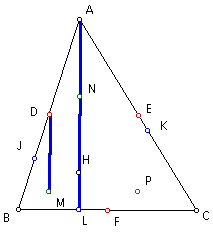
Since segment AL is perpendicular to side BC by construction (AL is the altitude from point A to side BC), and side BC is parallel to segment DE, then segment AL is perpendicular to segment DE.
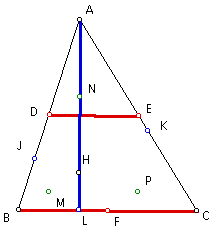
Since segment MD is parallel to segment AL, and segment AL is perpendicular to segment DE, then segment MD is perpendicular to segment DE.
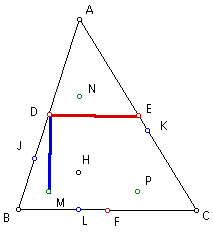
Thus, we have that quadrilateral DEPM is a rectangle. Since the opposite angles of this quadrilateral are supplementary, it follows that the quadrilateral can be inscribed in a circle.
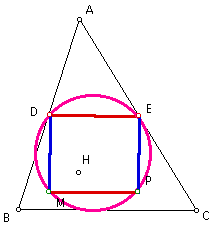
Similarly, quadrilateral DNPF is a rectangle, and it can be inscribed in a circle.
Therefore, points D, N, E, P, F, and M are on a common circle, with one diameter of the circle being segment DP, since this segment is a diagonal of both rectangles. The center of this circle, then, is the midpoint of segment DP. Let this center be point O.
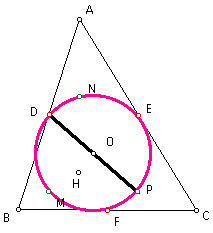
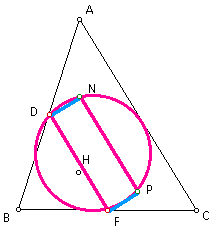
Now, since segment AL is an altitude, angle NLF is a right angle. But segment NF is also a diameter of our circle (it is a diagonal of rectangle DNPF), so it follows that point L must lie on this circle.
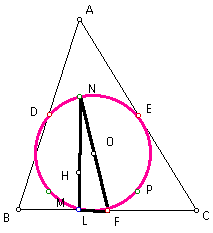
Similarly, points J and K are on the circle.
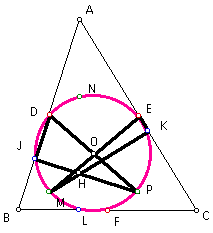
Therefore, all nine points D, E, F, J, K, L, M, N, and P lie on the same circle, called the nine-point circle. QED.