

In this write-up, I pose a solution to the following problem:
The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C. Does your result hold only for acute triangles?
First, I present a Geometer's SketchPad sketch of the situation when triangle ABC is an acute triangle. Next, I find the values of angle L, angle M, and angle N in terms of angles A, B, and C. Then I do a quick bit of algebra to double check my answer. Finally, I examine whether my result also holds for right and obtuse triangles.
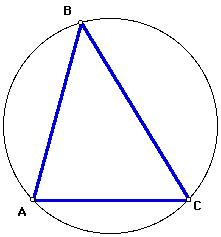
I started with acute triangle ABC and its circumcircle.
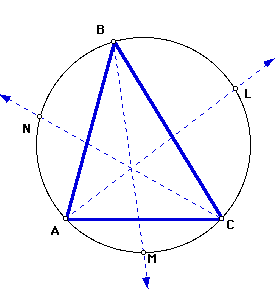
Next, I constructed the angle bisectors of each angle. Obviously, each angle bisector will intersect the circumcircle. I called the points of intersection of the circumcircle and the angle bisectors of angles A, B, and C points L, M, and N, respectively.
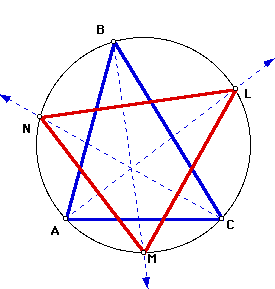
Finally, I connected points L, M, and N to form a new triangle. Since points L, M, and N are on the circumcircle, then it is obvious to see that triangle LMN is inscribed in the same circle as triangle ABC. This fact proves valuable to the proof.
The challenge is to write angles L, M, and N in terms of angles A, B, and C. Here is some background information used in finding a solution to the problem:
There is a theorem in geometry which states that when an inscribed angle and a central angle of a circle intercept a common arc of the circle, then the measure of the inscribed arc is half the measure of the central angle (click here to see a proof). A corollary of this theorem states that when two inscribed angles of a circle intercept a common arc, then the angles are equal (click here to see a proof). This corollary will be used extensively in finding a result for this problem.
Since ray BM is the angle bisector of angle B, then the measure of angle ABM = 1/2 of the measure of angle B. Since inscribed angles ABM and ALM intercept a common arc (see sketch below), by our corollary, the measure of angle ABM = the measure of angle ALM. By substitution, the measure of angle ALM = 1/2 of the measure of angle B.
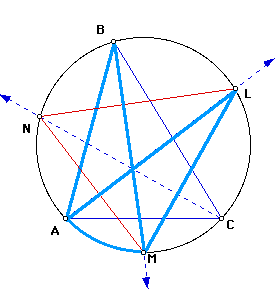
Since ray CN is the angle bisector of angle C, then the measure of angle ACN = 1/2 of the measure of angle C. Since inscribed angles ACN and ALN intercept a common arc (see sketch below), by our corollary, the measure of angle ACN = the measure of angle ALN. By substitution, the measure of angle ALN = 1/2 of the measure of angle C.
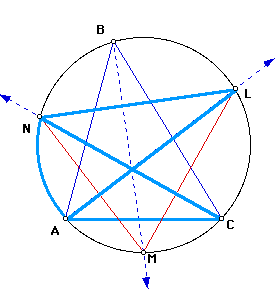
Finally, by angle addition, the measure of angle L = the sum of the measures of angle ALM and ALN. By subsitution, this means the measure of angle L = 1/2 of the measure of angle B + 1/2 of the measure of angle C.
Since ray AL is the angle bisector of angle A, then the measure of angle BAL = 1/2 of the measure of angle A. Since inscribed angles BAL and BML intercept a common arc (see sketch below), by our corollary, the measure of angle BAL = the measure of angle BML. By substitution, the measure of angle BML = 1/2 of the measure of angle A.
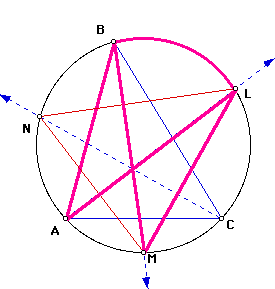
Since ray CN is the angle bisector of angle C, then the measure of angle BCN = 1/2 of the measure of angle C. Since inscribed angles BCN and BMN intercept a common arc (see sketch below), by our corollary, the measure of angle BCN = the measure of angle BMN. By substitution, the measure of angle BMN = 1/2 of the measure of angle C.
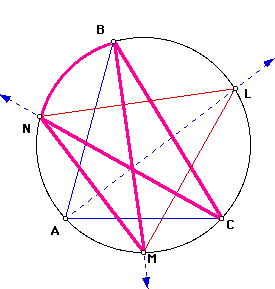
Finally, by angle addition, the measure of angle M = the sum of the measures of angle BML and BMN. By subsitution, this means the measure of angle M = 1/2 of the measure of angle A + 1/2 of the measure of angle C.
Since ray AL is the angle bisector of angle A, then the measure of angle CAL = 1/2 of the measure of angle A. Since inscribed angles CAL and CNL intercept a common arc (see sketch below), by our corollary, the measure of angle CAL = the measure of angle CNL. By substitution, the measure of angle CNL = 1/2 of the measure of angle A.
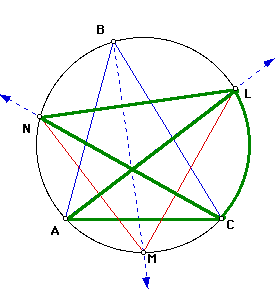
Since ray BM is the angle bisector of angle B, then the measure of angle CBM = 1/2 of the measure of angle B. Since inscribed angles CBM and CNM intercept a common arc (see sketch below), by our corollary, the measure of angle CBM = the measure of angle CNM. By substitution, the measure of angle CNM = 1/2 of the measure of angle B.
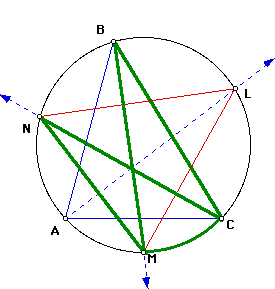
Finally, by angle addition, the measure of angle N = the sum of the measures of angle CNL and CNM. By subsitution, this means the measure of angle N = 1/2 of the measure of angle A + 1/2 of the measure of angle B.
I can quickly check my answer by performing a little bit of algebra. In summary, I found that the measure of angle L = 1/2 of the measure of angle B + 1/2 of the measure of angle C, the measure of angle M = 1/2 of the measure of angle A + 1/2 of the measure of angle C, and the measure of angle N = 1/2 of the measure of angle A + 1/2 of the measure of angle B.
Since I know that the sum of the angles of a triangle equal 180 degrees, it follows that the measure of angle L + the measure of angle M + the measure of angle N = 180 degrees. By substitution, (1/2 of the measure of angle B + 1/2 of the measure of angle C) + (1/2 of the measure of angle A + 1/2 of the measure of angle C) + (1/2 of the measure of angle A + 1/2 of the measure of angle B) = 180 degrees. Is this true?
Well, by combining like terms, I get the measure of angle A + the measure of angle B + the measure of angle C = 180 degrees. Since the sum of the angles in triangle ABC must equal 180 degrees, this checks!
By investigating with GSP, I conjecture that my result for acute triangles also holds for right and obtuse triangles.
Click here to manipulate the GSP file of this problem, and see if you agree.