

Here, I am given triangle ABC. Let P be a pedal point of triangle ABC. Let R be the foot of the altitude from P to side AB, S be the foot of the altitude from P to side BC, and T be the foot of the altitude from P to side AC. My conjecture states that pedal triangle RST is a degenerate triangle, i.e. a straight line, if and only if pedal point P lies on the circumcircle of triangle ABC.
First, I assume pedal point P lies on the circumcircle of triangle ABC, and I want to prove that pedal triangle RST is degenerate, i.e. it is a straight line.
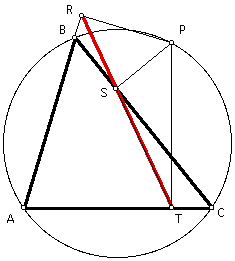
First, I construct segments PA, PB, and PC.
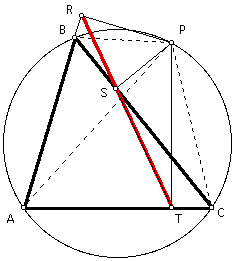
Now, notice that angle BRP is 90 degrees, angle BSP is 90 degrees, so triangles BRP and BSP are right. These right triangles share a common hypotenuse, segment BP. Therefore, segment BP is the diameter of a circle with angles BRP and BSP inscribed in this circle. It then follows that points B, R, P, and S are all on a common circle, and so quadrilateral BRPS is cyclic.
Since angles RSB and RPB are inscribed in this circle, and they intercept a common arc, then the measure of angle RSB equals the measure of angle RPB. Also, since the sum of the angles of triangle BRP is 180 degrees, and angle BRP is 90 degrees, then angles RBP and RPB are complementary.
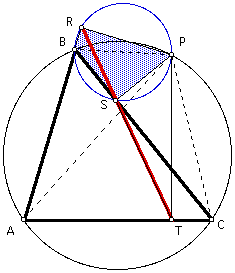
Similarly, notice that angle CSP is 90 degrees, angle CTP is 90 degrees, so triangles CSP and CTP are right. These right triangles share a common hypotenuse, segment CP. Therefore, segment CP is the diameter of a circle with angles CSP and CTP inscribed in this circle. It then follows that points C, T, S, and P are all on a common circle, and so quadrilateral CTSP is cyclic.
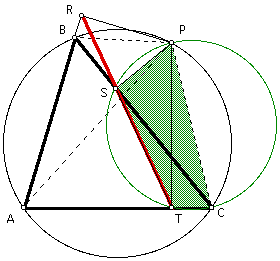
Since angles TSC and TPC are inscribed in this circle, and they intercept a common arc, then the measure of angle TSC equals the measure of angle TPC. Also, since the sum of the angles of triangle CTP is 180 degrees, and angle CTP is 90 degrees, then angles TPC and TCP are complementary.
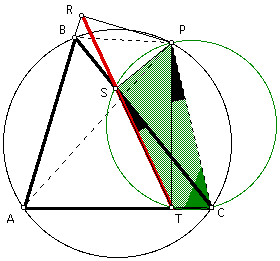
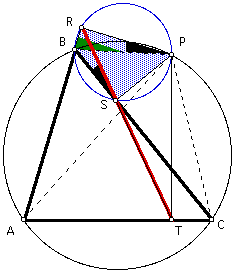
Now, since point P lies on the circumcircle of triangle ABC, then quadrilateral ABPC is cyclic. Therefore, opposite angles ABP and ACP are supplementary.
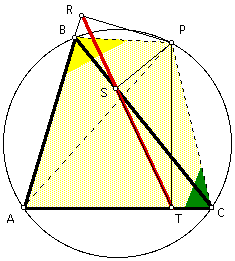
Since AR is a segment, then angles ABP and RBP are supplementary. Since angles RBP and ACP are supplementary to the same angle, it follows that the measure of angle RBP is equal to the measure of angle ACP.
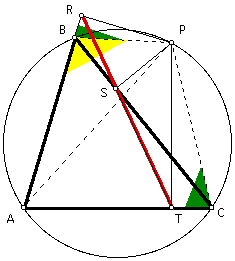
Now, the rest of the proof falls out nicely. Since angles ACP and TCP are the same, it follows that angles RBP and TCP are equal. Since angles RBP and RPB are complementary, and angles TCP and TPC are complementary, then angles RPB and TPC are complementary to equal angles, and so the measure of angle RPB is equal to the measure of angle TPC. Since angles RPB and RSB are equal, and angles TPC and TSC are equal, it follows that angles RSB and TSC are equal.
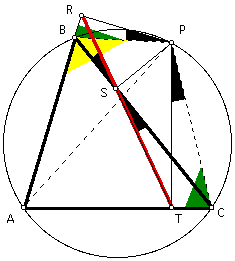
Therefore, angles RSB and TSC are vertical angles, and so angle RST must be straight. Therefore, pedal triangle RST is degenerate, i.e. it is a straight line. QED.
It remains to be proved that if pedal triangle RST is degenerate, i.e. a straight line, then pedal point P must lie on the circumcircle of triangle ABC.
This proof is actually a simple reverse of the above proof, so I'll leave it to the reader.