

Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
Starting with triangle ABC as an acute triangle, it seems that the products of (AF)(BD)(CE) and (AE)(CD)(BF) are equal.
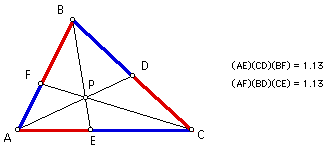
Moving P results in the products being still equal...
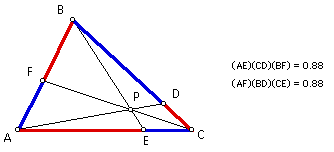
...and still equal again.
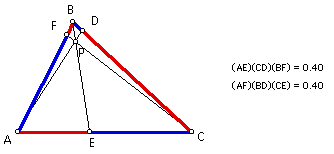
When triangle ABC is right, the products are equal.
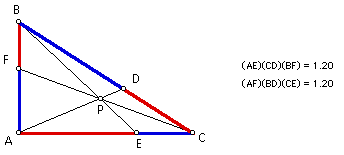
And when triangle ABC is obtuse, the products remain equal!!
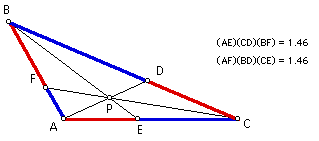
Therefore, I would conjecture that the products are always equal in the given situation.
Click here for a GSP sketch to manipulate if you need further convincing.
Conjecture? Prove it (you may need draw some parallel lines to produce some similar triangles)! Also, it probably helps to consider the ratio (FB)(DC)(EA)/(AF)(BD)(EC).
Based on my investigations of the situation with GSP, I conjecture that (BF*CD*AE)/(AF*BD*CE) = 1. My proof follows.
Given any triangle ABC and a point P inside the triangle. Let line AP intersect side BC in point D, line BP intersect side AC in point E, and line CP intersect side AB in point F. Prove (BF*CD*AE)/(AF*BD*CE) = 1.
First, I make some construction lines. I construct a line parallel to side AB through point C. Then, I extend segment AD and call its point of intersection with this parallel line point G. Finally, I extend segment BE and call its point of intersection with this parallel line point H.
As a result of drawing these construction lines, I get many pairs of similar triangles. These four pairs are important for my proof:
First, triangles AFP and GCP are similar by AA similarity. This is because angles FPA and CPG are congruent because they are vertical angles, and angles FAP and CGP are congruent because they are alternate interior angles.
Next, triangles BFP and HCP are similar by AA similarity. This is because angles FPB and CPH are congruent because they are vertical angles, and angles FBP and CHP are congruent because they are alternate interior angles.
Also, triangles ABD and GCD are similar by AA similarity. This is because angles BDA and CDG are congruent because they are vertical angles, and angles ABD and GCD are congruent because they are alternate interior angles.
Finally, triangles ABE and CHE are similar by AA similarity. This is because angles AEB and CEH are congruent because they are vertical angles, and angles ABE and CHE are congruent because they are alternate interior angles.
Now, by definition of similar triangles, I can state the following proportions:
Because triangles AFP and GCP are similar, AF/GC = FP/CP.
Because triangles BFP and HCP are similar, BF/HC = FP/CP.
Because triangles ABD and GCD are similar, GC/AB = CD/BD.
And because triangles ABE and CHE are similar, AB/HC = AE/CE.
The rest of the proof is mere algebra steps:
Multiplying the last three proportions together gives (BF/HC)*(AE/CE)*(CD/BD) = (FP/CP)*(AB/HC)*(GC/AB).
After cross-canceling AB on the right side of the equation and eliminating the common HC in the denominator in both sides of the equation, I get (BF)*(AE/CE)*(CD/BD) = (FP/CP)*(GC).
Then substituting AF/GC for FP/CP (from the first original proportion) gives (BF)*(AE/CE)*(CD/BD) = (AF/GC)*(GC). This allows the GC to cross-cancel on the right side of the equation, leaving (BF)*(AE/CE)*(CD/BD) = AF.
Dividing both sides of the equation by AF gives (BF*AE*CD)/(AF*CE*BD) = 1, which was to be proved. QED.
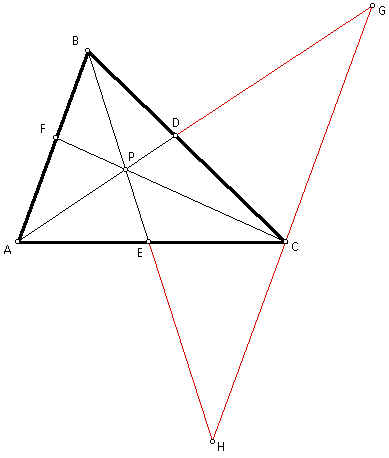
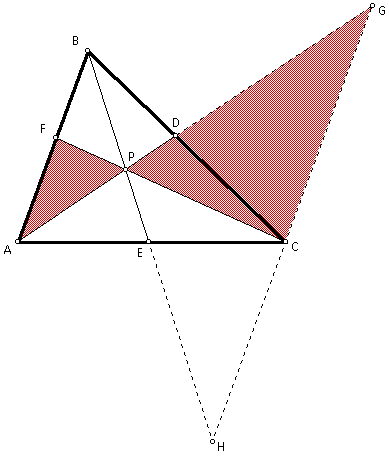
Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle? Show a working GSP sketch.
I would conjecture that the result can be generalized so that P can be outside the triangle.
Click here for a GSP sketch of this situation to manipulate.
Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to4.
Here is an example when the ratio is greater than 4:
Here is another example:
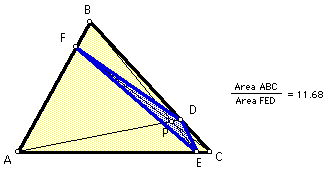
And another:

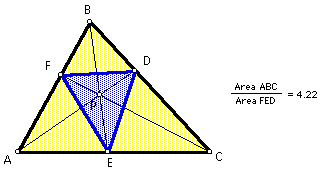
Finally, here is an example when the ratio is equal to 4:
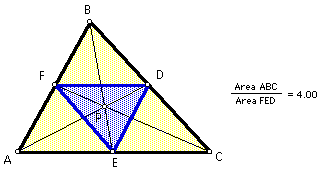
It seems that the above conjecture is always true.
Click here for a GSP sketch to manipulate if you need further convincing.
When is the ratio equal to 4?
I conjecture that the ratio is equal to 4 if P is the centroid of triangle ABC.
On a side note, here is a quick proof:
By definition, when P is the centroid of triangle ABC, point D is the midpoint of side BC, point E is the midpoint of side AC, and point F is the midpoint of side AB.
Therefore, triangles ABC and AFE are similar by SAS similarity, because angle A is congruent in each triangle, and AB/AF = AC/AE = 2.
Triangles ABC and FBD are similar by SAS similarity, because angle B is congruent in each triangle, and AB/FB = BC/BD = 2.
And triangles ABC and EDC are similar by SAS similarity, because angle C is congruent in each triangle, and AC/EC = BC/DC = 2.
By the definition of similarity, it follows that AB/DE = BC/EF = AC/DF = 2. Thus, triangles ABC and DEF are similar by SSS similarity.
Since all four of the smaller triangles are similar to triangle ABC by the same scale ratio, it follows that triangles AFE, FBD, EDC, and DEF are congruent. This also means that the areas of each of the four smaller triangles are equal.
Finally, the area of triangle ABC = area of triangle AFE + area of triangle FBD + area of triangle EDC + area of triangle DEF. By subsitution, the area of triangle ABC = 4*(area of triangle DEF), which was to be proved. QED.
I conjecture that this theorem should actually be an "if and only if" theorem. In other words, I also think that if the scale ratio is equal to 4, then P must be the centroid of the triangle. But since a proof is not actually required in this part of the assignment, I think I will stop here and leave this proof to the reader!