Objectives: To find the amplitude and period of a trigonometric function from its equation; to find the amplitude and period of a trigonometric function from its graph; to graph sine and cosine functions with various amplitudes and periods.
"Amplitude and frequency are important concepts that are essential to the understanding of many fields, including music.
"The loudness, or amplitude, or a musical sound is a comparative measure of the strength of the sound that is heard. Loudness is related to the distance from the source and the energy of the vibration.
"Pitch is determined by the number of vibrations per second, or the frequency of the vibrations that yield a sound wave. Frequency is the reciprocal of the period."
Resource: Hayden, Jerome D. and Hall, Bettye C. (1993). Trigonometry. Prentice Hall: Englewood Cliffs, New Jersey.
I. Graphing amplitude in sine functions.
1. Graph y = sinx in Graphing Calculator.
2. Go to the "Math" Menu and choose "New Math Expression". Graph y = 2sinx. How does the graph of y = 2sinx differ from the graph of y = sinx?
3. Delete the equation y = 2sinx. Graph y = 0.5sinx. How does the graph of y = 0.5sinx differ from the graph of y = sinx?
4. Delete the equation y = 0.5sinx. Graph y = -sinx. How does the graph of y = -sinx differ from the graph of y = sinx?
5. Delete the equations y = sinx and y = -sinx. Graph the equation y = nsinx, letting n vary from -10 to 10. Animate. What effect does "n" have on the graphs?
II. Graphing amplitude in cosine functions.
Graph y = ncosx, letting n vary from -10 to 10. Animate. Does the graph of y = ncosx react to the values of n the same way the graph of y = nsinx did?
III. Making sense of amplitude.
1. Answer the following questions about equations in the forms y = Asinx and y = Acosx:
a) What happens to the graph of y = sinx and y = cosx when A > 1?
b) What happens when 0 < A < 1?
c) When -1 < A < 0?
d) What about when A = -1?
e) And when A < -1?
2. Define amplitude.
3. By only looking at the equations in the form y = Asinx or y = Acosx (and not graphing), can you write an expression that gives the amplitude of the graph?
4. By only looking at the graphs of the equations in the form y = Asinx or y = Acosx (and not knowing the exact equation), can you write an expression that gives the amplitude of the graph?
I.
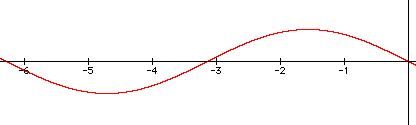
1. Here is a sample graph:
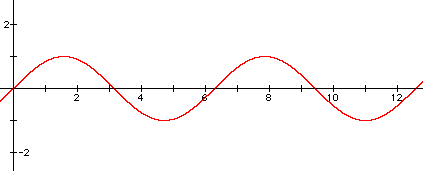
2. Here is a sample graph and answer:
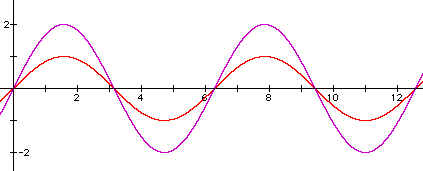
3. Here is a sample graph and answer:
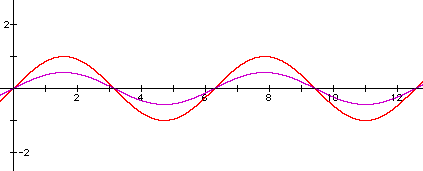
4. Here is a sample graph and answer:
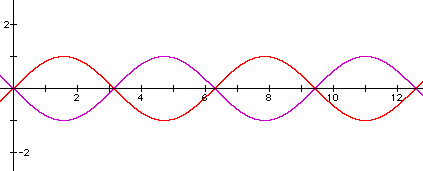
5. Click HERE to see a sample animation. Answer: The graphs get "taller" or "shorter."
II. Click HERE to see a sample animation. Answer: Yes.
III.
1. Here are sample answers:
a) The graph gets "taller" by A.
b) The graph gets "shorter" by A.
c) The graph flips around the x-axis and gets "shorter" by A.
d) The graph flips around the x-axis.
e) The graph flips around the x-axis and gets "taller" by A.
2. Amplitude is "related to the height of the graph."
3. Amplitude = | A |
4. Amplitude = 0.5(M-m), where M is the maximum value of the range and m is the minimum value of the range.
I. Graphing period in cosine functions.
1. Graph y = cosx in Graphing Calculator.
2. Go to the "Math" Menu and choose "New Math Expression". Graph y = cos2x. How does the graph of y = cos2x differ from the graph of y = cosx?
3. Delete the equation y = cos2x. Graph y = cos0.5x. How does the graph of y = cos0.5x differ from the graph of y = cosx?
4. Delete the equation y = cosx. Graph y = cos(-x). How does the graph of y = cos(-x) differ from the graph of y = cosx?
5. Delete the equations y = cosx and y = cos(-x). Graph the equation y = cosnx, letting n vary from -10 to 10. Animate. What effect does "n" have on the graphs?
II. Graphing period in sine functions.
Graph y = sinnx, letting n vary from -10 to 10. Animate. Does the graph of y = sinnx react to the values of n the same way the graph of y = cosnx did?
III. Making sense of period.
1. Answer the following questions about equations in the forms y = sinBx and y = cosBx:
a) What happens to the graphs of y = sinx and y = cosx when B > 1?
b) What happens when 0 < B < 1?
c) When -1 < B < 0? Be careful!!
d) What about when B = -1? Be careful!!
e) And when B < -1? Be careful!!
2. Define period.
3. By only looking at the equations in the form y = sinBx or y = cosBx (and not graphing), can you write an expression that gives the period of the graph?
4. By only looking at the graphs of the equations in the form y = sinBx or y = cosBx (and not knowing the exact equation), can you write an expression that gives the period of the graph?
I.
1. Here is a sample graph:
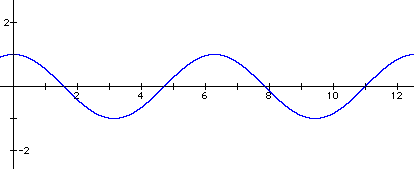
2. Here is a sample graph and answer:
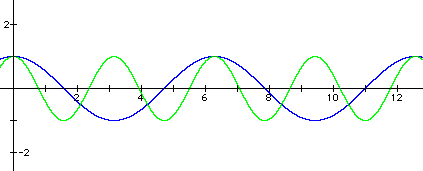
3. Here is a sample graph and answer:

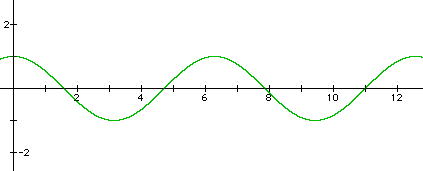
4. Here is a sample graph and answer:
5. Click HERE to see a sample animation. Answer: The graph gets "squeezed" or "stretched."
II. Click HERE to see a sample animation. Answer: Yes, except for one difference. When n is negative, y = sinnx "flips" about the x-axis but y = cosnx does not. (This is because sin(-x) = -sinx and cos(-x) = cosx).
III.
1. Here are sample answers:
a) The graph gets "squeezed" by B.
b) The graph gets "stretched" by B.
c) For y = sinBx, the graph flips about the x-axis and gets "stretched" by B. For y = cosBx, the graph gets "stretched" by B.
d) For y = sinBx, the graph flips about the x-axis. For y = cosBx, the graph remains the same.
e) For y = sinBx, the graph flips about the x-axis and gets "squeezed" by B. For y = cosBx, the graph gets "squeezed" by B.
2. Period is one complete cycle or pattern of the graph.
3. Period = 2p / | B |
4. Period = | N - n |, where n is the x-value of any point on the graph and N is the x-value of a second point on the graph, found by tracing the graph until the pattern starts to repeat.
1. Determine the amplitude and period of each function.
a) y = sin4x
b) y = -4cos5x
c) y = -2cos(5/4)x
d) y = 3cos(-2x)
2. Determine the amplitude and period of each function. Then write an equation of each graph.
a)
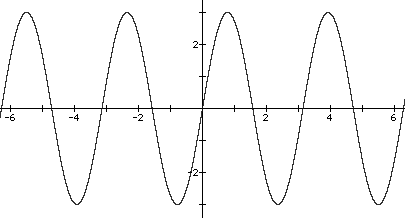
b)
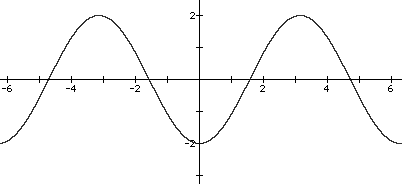
3. Give the amplitude and period of each function. Then sketch the graph of the function over the given interval.
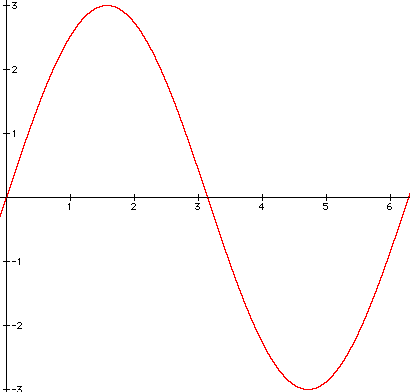
a) y = 3sinx, [0, 2p]
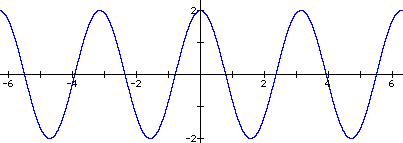
b) y = 2cos2x, [-2p, 2p]
c) y = -cos0.5x, [-p, p]
d) y = 0.5sin(-x), [-2p, 0]
1.
a) amp = 1, pd = p/ 2
b) amp = 4, pd = 2p/5
c) amp = 2, pd = 8p/5
d) amp = 3, pd = p
2.
a) amp = 3, pd = p, y = 3sin2x
b) amp = 2, pd = 2p, y = -2cosx
3.
a) amp = 3, pd = 2p
b) amp = 2, pd = p
c) amp = 1, pd = 4p
d) amp = 0.5, pd = 2p