Objectives: To find the phase shift and the vertical shift of sine and cosine functions from their equations; to find the phase shift and vertical shift of sine and cosine functions from their graphs; to graph sine and cosine functions with various phase shifts and vertical shifts.
In the previous lesson, students learned that amplitude and period make the graphs of sine and cosine functions get taller, shorter, stretched, and squeezed. All of these changes affected the "SHAPE" of a graph. In this lesson, students will examine how phase shift and vertical shift affect the "LOCATION" of a graph.
I. Graphing phase shift in sine functions.
1. Graph y = sinx in Graphing Calculator.
2. Go to the "Math" Menu and choose "New Math Expression". Graph y = sin(x + p/4). How does the graph of y = sin(x + p/4) differ from the graph of y = sinx?
3. Delete the equation y = sin(x + p/4). Graph y = sin(x - p/ 2). How does the graph of y = sin(x - p/ 2) differ from the graph of y = sinx?
4. Delete the equation y = sin(x - p/ 2). Graph y = sin(x + p). How does the graph of y = sin(x + p) differ from the graph of y = sinx? Be careful!!
5. Delete the equations y = sinx and y = sin(x + p). Graph the equation y = sin(x + n), letting n vary from -10 to 10. Animate. What effect does "n" have on the graphs?
II. Graphing phase shift in cosine functions.
Graph y = cos(x + n), letting n vary from -10 to 10. Animate. Does the graph of y = cos(x + n) react to the values of n the same way the graph of y = sin(x + n) did?
III. Making sense of phase shift.
1. Answer the following questions about equations in the forms y = sin(x + C) and y = cos(x + C):
a) What happens to the graph of y = sinx and y = cosx when C is positive?
b) What about when C is negative?
2. Define phase shift.
I.
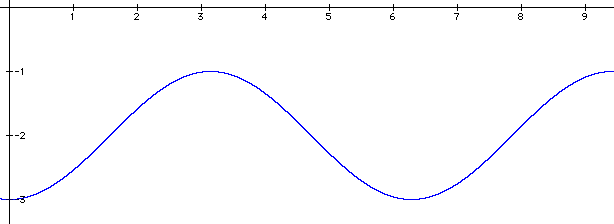
1. Here is a sample graph:
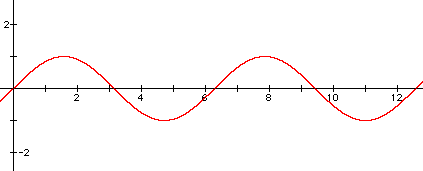
2. Here is a sample graph and answer:
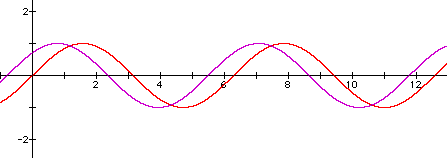
3. Here is a sample graph and answer:
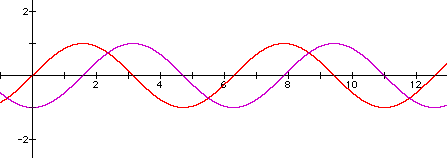
4. Here is a sample graph and answer:
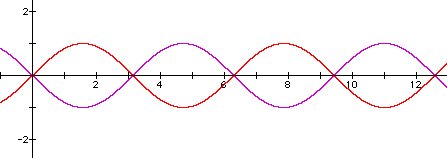
5. Click HERE to see a sample animation. Answer: The graph moves left and right.
II. Click HERE to see a sample animation. Answer: Yes.
III.
1. Here are sample answers:
a) The graph moves left C units.
b) The graph moves right C units.
2. A phase shift is a horizontal shift (right or left) of the graph.
I. Graphing vertical shift in cosine functions.
1. Graph y = cosx in Graphing Calculator.
2. Go to the "Math" Menu and choose "New Math Expression". Graph y = cosx + 2. How does the graph of y = cosx + 2 differ from the graph of y = cosx?
3. Delete the equation y = cosx + 2. Graph y = cosx - 1. How does the graph of y = cosx - 1 differ from the graph of y = cosx?
4. Delete the equations y = cosx and y = cosx - 1. Graph the equation y = cosx + n, letting n vary from -10 to 10. Animate. What effect does "n" have on the graphs?
II. Graphing vertical shift in sine functions.
Graph y = sinx + n, letting n vary from -10 to 10. Animate. Does the graph of y = sinx + n react to the values of n the same way the graph of y = cosx + n did?
III. Making sense of period.
1. Answer the following questions about equations in the forms y = sinx + D and y = cosx + D:
a) What happens to the graphs of y = sinx and y = cosx when D is positive?
b) What about when D is negative?
2. Define vertical shift.
I.
1. Here is a sample graph:
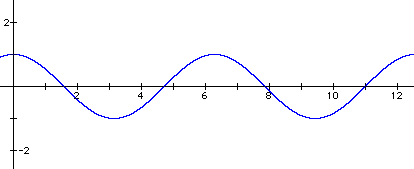
2. Here is a sample graph and answer:
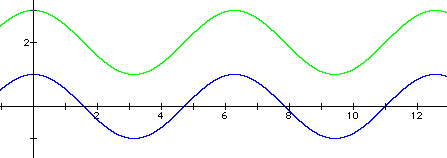
3. Here is a sample graph and answer:
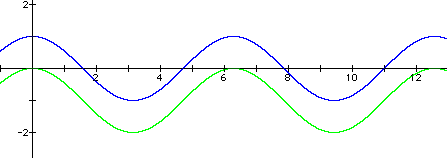
4. Click HERE to see a sample animation. Answer: The graph moves up and down.
II. Click HERE to see a sample animation. Answer: Yes.
III.
1. Here are sample answers:
a) The graph moves up D units.
b) The graph moves down D units.
2. A vertical shift is when the graph moves up or down.
1. Determine the amplitude, period, phase shift, and vertical shift of each function.
a) y = cos2x - 5
b) y = 2sin(3x + 3p)
c) y = 3cos0.5x + 4
d) y = -sin(x - p/4) - 2
2. Determine the phase shift and vertical shift of each function. Then write an equation of each graph.
a)
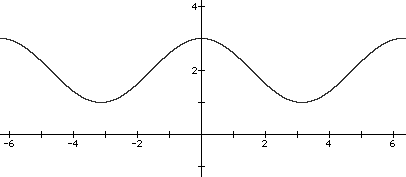
b)
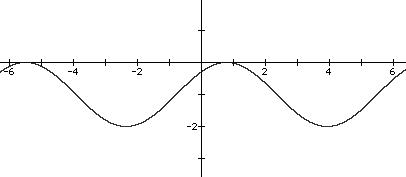
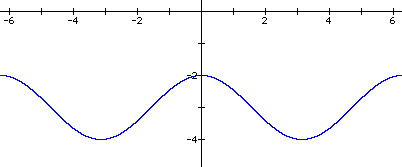
3. Give the phase shift and vertical shift of each function. Then sketch the graph of the function over the given interval.
a) y = sin(x - p/ 2) + 1, [0, 2p]
b) y = cosx - 3, [-2p, 2p]
c) y = cos(x + p) - 2, [0, 3p]
1.
a) amp = 1, pd = p, ps = 0, vs = 5 down
b) (First factor out 3: y = 2sin3(x + p)) amp = 2, pd = 2p/3, ps = p left, vs = 0
c) amp = 3, pd = 4p, ps = 0, vs = 4 up
d) amp = 1, pd = 2p, ps = p/4 right, vs = 2 down
2.
a) ps = 0, vs = 2, y = cosx + 2 OR ps = p/2 left, vs = 2, y = sin(x + p/2) + 2
b) ps = p/4 right, vs = 1 down, y = cos(x - p/4) - 1 OR ps = p/2 left, vs = 1 down, y = sin(x + p/2) - 1
3.
a) ps = p/ 2 right, vs = 1 up
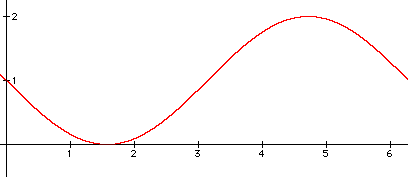
b) ps = 0, vs = 3 down
c) ps = p left, vs = 2 down