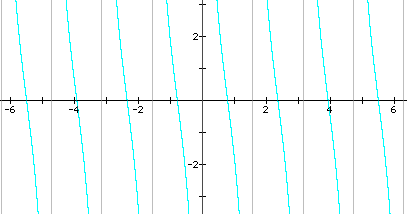
Objectives: To determine the properties of the tangent and cotangent functions; to graph the tangent and cotangent functions.
I. First, let's set up and examine a table of the coordinates of some of the points that will satisfy the equation y = tanx.
1. Open an Excel spreadsheet. Label column A "x-coordinates" and column B "y-coordinates." Set both columns to round to 4 decimal places.
2. Fill in your x-coordinates in column A by ranging from -2p to 2p by increments of p/ 4. Remember, x represents an angular measure - we're using radians as our units.
3. Fill in your y-coordinates in column B by utilizing the equation, y = tanx.
What do you notice about the values in this column? What does the ##### mean? Can you predict what the graph will look like?
II. Graphing in Graphing Calculator.
1. Graph y = tanx from -2p to 2p.
2. Explain what the vertical lines on the graph represent.
3. What is the length of one period of y = tanx?
4. Do tangent graphs have "amplitude?" Why or why not?
III. Check yourself.
Sketch (by hand!) what the graph of y = tanx will look like, given the following domain restrictions. Be careful about where the graph crosses the x-axis, where the points of inflection are, and where the asymptotes are.
a) 2p to 4p
b) -4p to 0
c) -3p/2 to p/2
I.
2. In cell A2, type in "=-2*pi()". In cell A3, type in "=A2+pi()/ 4". Drag to fill down to row 18.
3. In cell B2, type in "=tan(A2)". Drag to fill down to row 18.
Here is a sample table:
|
|
|
| -6.2832 | 0 |
| -5.4978 | 1 |
| -4.7124 | ##### |
| -3.9270 | -1 |
| -3.1416 | 0 |
| -2.3562 | 1 |
| -1.5708 | ##### |
| -0.7854 | -1 |
| 0 | 0 |
| 0.7854 | 1 |
| 1.5708 | ##### |
| 2.3562 | -1 |
| 3.1416 | 0 |
| 3.9270 | 1 |
| 4.7124 | ##### |
| 5.4978 | -1 |
| 6.2832 | 0 |
Answers: The values in the y-coordinates column repeat. The ##### means "undefined."
II.
1. Here is a sample graph:

2. The vertical lines are asymptotes of the graph.
3. One period = p.
4. No. Tangent graphs go on forever in vertical directions, so they cannot have a "height."
III.
a)
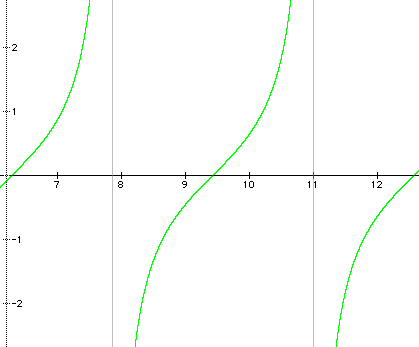
b)
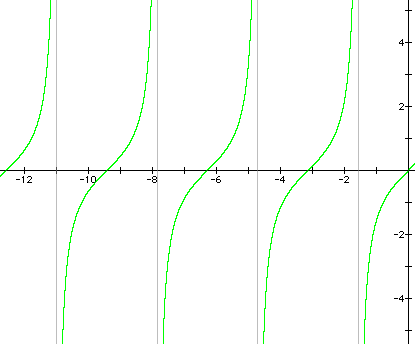
c)
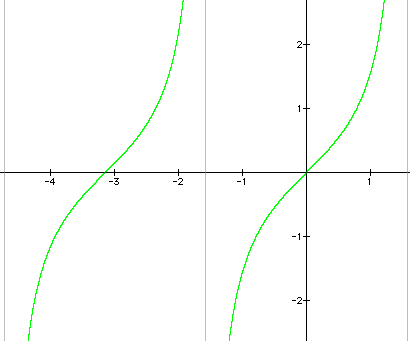
I. First, let's set up and examine a table of the coordinates of some of the points that will satisfy the equation y = cotx.
1. Open an Excel spreadsheet. Label column A "x-coordinates" and column B "y-coordinates." Set both columns to round to 4 decimal places.
2. Fill in your x-coordinates in column A by ranging from -2p to 2p by increments of p/ 4. Remember, x represents an angular measure - we're using radians as our units.
3. Fill in your y-coordinates in column B by utilizing the equation, y = cotx. Remember that cotx is the reciprocal of tanx.
What do you notice about the values in this column? What does the ##### mean? Can you predict what the graph will look like?
How do the y-coordinates in this table relate to the y-coordinates in the table for y = tanx?
II. Graphing in Graphing Calculator.
1. Graph y = cotx from -2p to 2p.
2. Explain what the vertical lines on the graph represent.
3. What is the length of one period of y = cotx?
4. Do cotangent graphs have "amplitude?" Why or why not?
5. How does this graph relate to the graph of y = tanx?
III. Check yourself.
Sketch (by hand!) what the graph of y = cotx will look like, given the following domain restrictions. Be careful about where the graph crosses the x-axis, where the points of inflection are, and where the asymptotes are.
a) 2p to 4p
b) -4p to 0
c) -3p/2 to p/2
I.
2. In cell A2, type in "=-2*pi()". In cell A3, type in "=A2+pi()/ 4". Drag to fill down to row 18.
3. In cell B2, type in "=1/(tan(A2))". Drag to fill down to row 18.
Here is a sample table:
x-coordinates y-coordinates -6.2832 ##### -5.4978 1 -4.7124 0 -3.9270 -1 -3.1416 ##### -2.3562 1 -1.5708 0 -0.7854 -1 0 ##### 0.7854 1 1.5708 0 2.3562 -1 3.1416 ##### 3.9270 1 4.7124 0 5.4978 -1 6.2832 ##### Answers: The values in the y-coordinates column repeat. The ##### mean "undefined."
The y-coordinates in this table are simply the reciprocals of the y-coordinates in the table for y = tanx.
II.
1. Here is a sample graph:
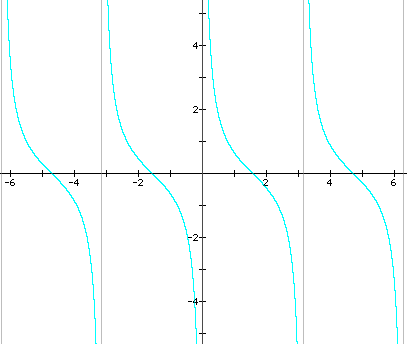
2. The vertical lines are asymptotes of the graph.
3. One period = p.
4. No. Cotangent graphs go on forever in vertical directions, so they cannot have a "height."
5. The x-intercepts of the graph of y = tanx become asymptotes in the graph of y = cotx. The asymptotes of the graph y = tanx become x-intercepts in the graph of y = cotx. The points that have y-coordinates of 1 and -1 have the same x-coordinates, respectively, in the graphs of both y = tanx and y = cotx. Essentially, the graphs "face" opposite directions - y = tanx to the right and y = cotx to the left.
III.
a)
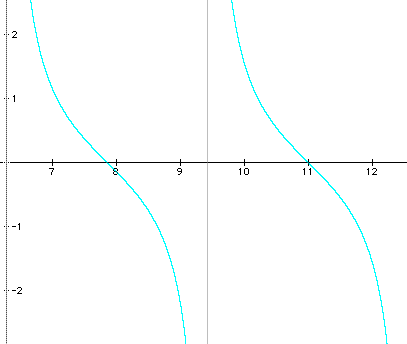
b)
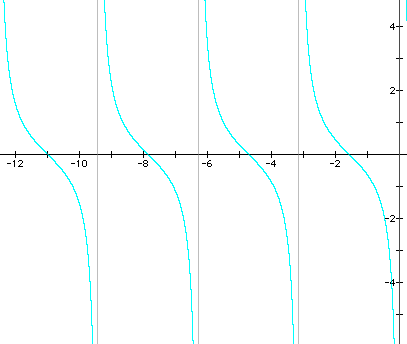
c)
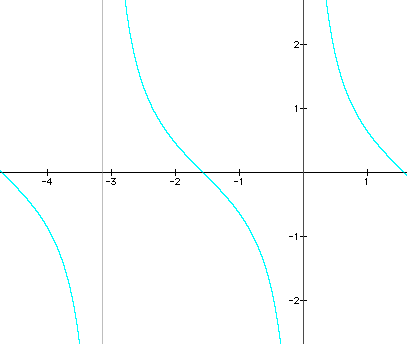
I. Using Graphing Calculator,
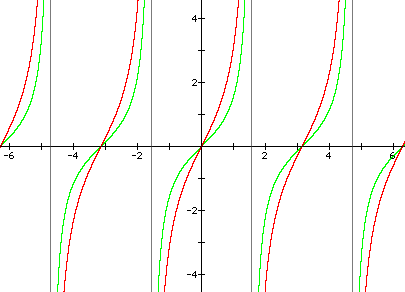
1. Graph y = tanx and y = 2tanx on the same coordinate plane (but in different colors).
2. Then graph y = cotx and y = -0.5cotx on the same coordinate plane (but in different colors).
Examine more graphs of this form if you find it necessary to be able to answer the following questions.
Answer the following questions about equations in the forms y = Atanx and y = Acotx:
a) What happens to the graph of y = tanx and y = cotx when A > 1?
b) What happens when 0 < A < 1?
c) When -1 < A < 0?
d) What about when A = -1?
e) And when A < -1?
II. Using Graphing Calculator,
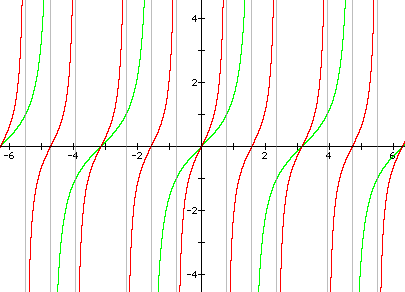
1. Graph y = tanx and y = tan2x on the same coordinate plane (but in different colors).
2. Then graph y = cotx and y = cot0.5x on the same coordinate plane (but in different colors).
Examine more graphs of this form if you find it necessary to be able to answer the following questions.
Answer the following questions about equations in the forms y = tanBx and y = cotBx:
a) What happens to the graphs of y = tanx and y = cotx when B > 1?
b) What happens when 0 < B < 1?
c) When -1 < B < 0?
d) What about when B = -1?
e) And when B < -1?
f) How can you figure out the period of a function, based on its equation?
III. Using Graphing Calculator,
1. graph y = tanx and y = tan(x - p/2) on the same coordinate plane (but in different colors).
2. Then graph y = cotx and y = cot(x + p/4) on the same coordinate plane (but in different colors).
Examine more graphs of this form if you find it necessary to be able to answer the following questions.
Answer the following questions about equations in the forms y = tan(x + C) and y = cot(x + C):
a) What happens to the graph of y = tanx and y = cotx when C is positive?
b) What about when C is negative?
IV. Using Graphing Calculator,
1. Graph y = tanx and y = tanx + 2 on the same coordinate plane (but in different colors).
2. Then graph y = cotx and y = cotx - 1 on the same coordinate plane (but in different colors).
Examine more graphs of this form if you find it necessary to be able to answer the following questions.
Answer the following questions about equations in the forms y = tanx + D and y = cotx + D:
a) What happens to the graphs of y = tanx and y = cotx when D is positive?
b) What about when D is negative?
(Note: All y = tanx graphs are green and their paired graphs are red; all y = cotx graphs are turquoise and their paired graphs are purple)
I. Here are some sample graphs:
1.
2.
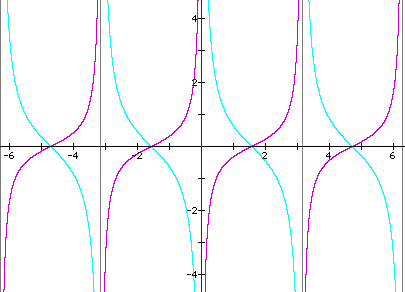
a) The graphs "stretch" away from the x-axis.
b) The graphs "shrink" toward the x-axis.
c) The graphs "flip" about the x-axis and "shrink" toward the x-axis.
d) The graphs "flip" about the x-axis.
e) The graphs "flip" about the x-axis and "stretch" away from the x-axis.
II. Here are some sample graphs:
1.
2.
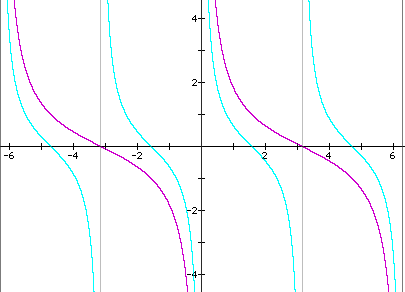
a) The graphs "squeeze" horizontally.
b) The graphs "stretch" horizontally.
c) The graphs "flip" about the x-axis and "stretch" horizontally.
d) The graphs "flip" about the x-axis.
e) The graphs "flip" about the x-axis and "squeeze" horizontally.
f) Period = p / | B |
III. Here are some sample graphs:
1.
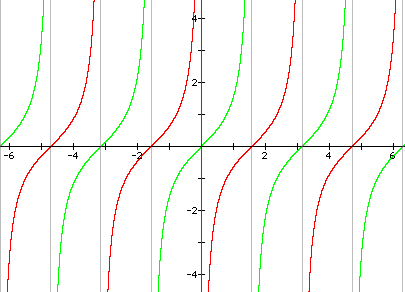
2.
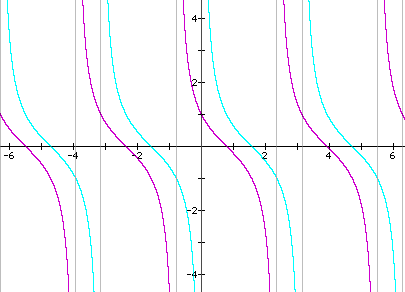
a) The graph moves C units to the left.
b) The graph moves C units to the right.
IV. Here are some sample graphs:
1.
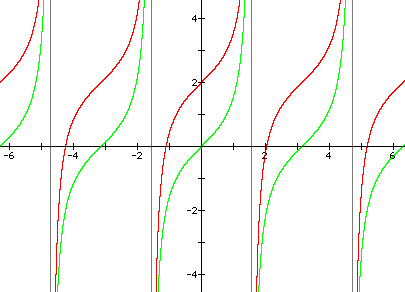
2.
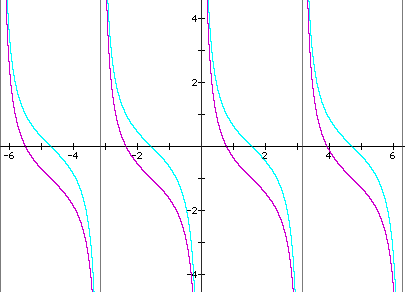
a) The graph moves D units up.
b) The graph moves D units down.
1. Determine the vertical stretching/shrinking, period, phase shift, and vertical shift of each function.
a) y = tan2(x + p) + 3
b) y = 5cot(x + 2p/3)
c) y = cot3(x - p) - 5
d) y = 3tan4x + 1
2. Graph each function over the interval [-2p, 2p] (Remember to graph by stages if necessary).
a) y = 2cotx -3
b) y = tan(x - p)
c) y = tan(x + p/2) +1
d) y = 4cot2x
1.
a) none, pd = p/2, ps = p left, vs = 3 up
b) v. stretch = 5, pd = p, ps = 2p/3left, vs = 0
c) none, pd = p/3, ps = p right, vs = 5 down
d) v. stretch = 3, pd = p/4, ps = 0, vs = 1 up
2.
a)
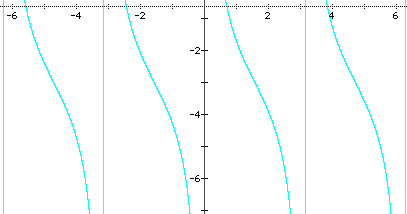
b)
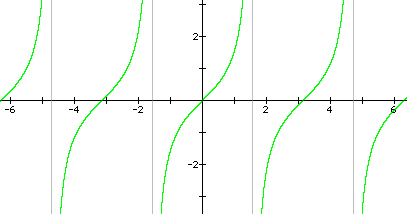
c)
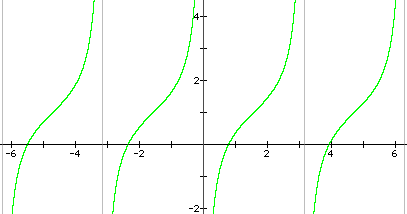
d)