

In general, a spiral is a curve on a plane which winds about a fixed point. There are many different types of spirals, some more interesting than others. In this essay, I have presented seven of the most recognized types of spirals.
Resources:
Chanan, Steven, ed. (2000). 101 Project Ideas for the Geometer's Sketchpad. Key Curriculum Press: Emeryville, CA.
Famous Curves Index. University of St. Andrews, Scotland. (http://www-groups.dcs.st-andrews.ac.uk/~history/Curves/Curves.html)
This spiral was described by Archimedes in his 225 BC work, On Spirals.
In the Spiral of Archimedes, each turn of the spiral is the same distance from the previous turn. The curve is actually the path of a point that moves outward from a central point along a ray at uniform speed as the ray rotates about the pole at a constant angular speed.
These spirals can be graphed using polar equations of the form r = aq.
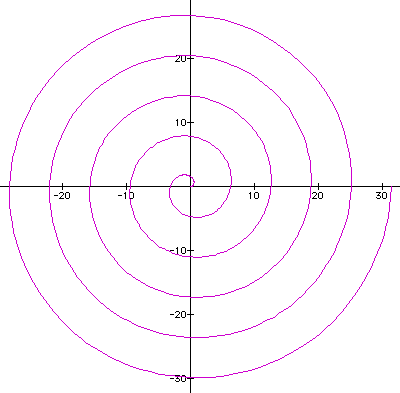
If you have Graphing Calculator, click HERE to see an animation of r = aq as "a" varies.
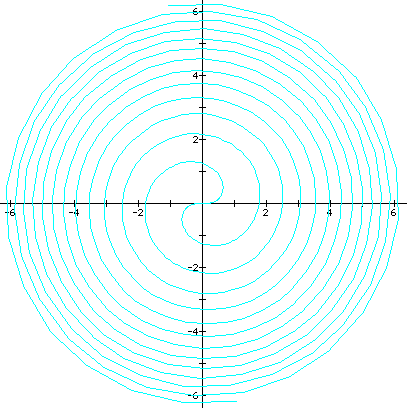
The Hyperbolic Spiral is the inverse of the Spiral of Archimedes. It was studied by Pierre Varignon in 1704.
These spirals can be graphed using polar equations of the form r = a/q. As q increases, the spiral winds around the origin and moves closer to it, and as q decreases, the spiral approaches the horizontal asymptote, y = a.
If you have Graphing Calculator, click HERE to see an animation of r = a/q as "a" varies.
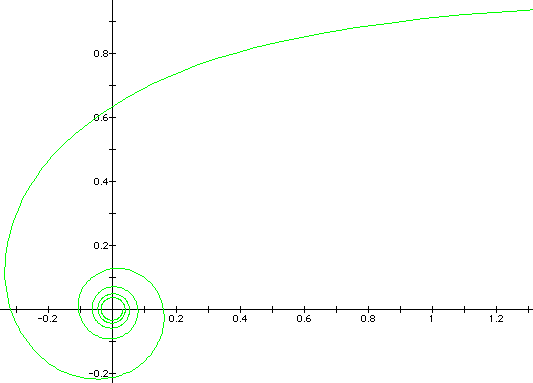
This spiral was discovered by Descartes in 1638. It occurs in the natural world in such places as the seashell of the many-chambered Nautilus.
The Logarithmic Spiral is also called the Equiangular Spiral because for any point on the spiral, the angle between the tangent line and the line to the origin is always the same.
These spirals can be graphed using polar equations of the form logr = aq.
If you have Graphing Calculator, click HERE to see an animation of logr = aq as "a" varies.
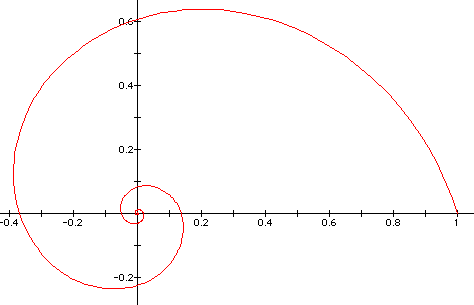
This spiral was described by Fermat in 1636.
These spirals can be graphed using polar equations of the form r^2 = (a^2)q.
If you have Graphing Calculator, click HERE to see an animation of r^2 = (a^2)q as "a" varies.
The Lituus is the inverse of Fermat's Spiral. It was studied by Cotes in 1722.
These spirals can be graphed using polar equations of the form r^2 = a^2/q.

If you have Graphing Calculator, click HERE to see an animation of r^2 = a^2/q as "a" varies.
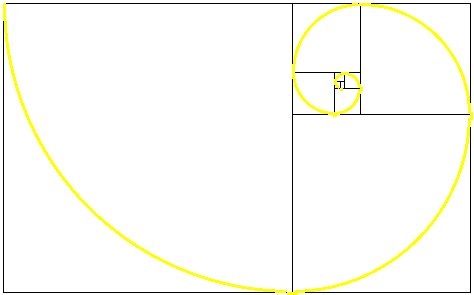
Golden Spirals are created by constructing quarter-circles inside the squares of Golden Rectangles.
Golden Rectangles are rectangles in which the ratio of their length to their width is the golden ratio. They have the special property that when a square is cut off, the remaining shape is another Golden Rectangle.
The Golden Spiral below was created on The Geometer's Sketchpad using an iterative process.
Click HERE for a GSP script of a Golden Spiral.
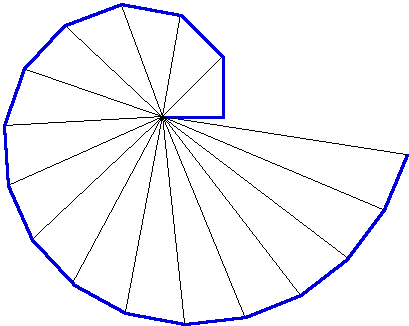
Square Root Spirals consist of right triangles, like in the figure below, in which each outer (thick blue) segment and the horizontal (thick blue) segment near the center are of equal length.
Square Root Spirals got their name from the following fact: If the blue segments are each = 1 unit, and Ni represents the length of the hypotenuse in the ith right triangle (starting from the center), then Ni = sqrt[(Ni-1 )^2 + 1], where i is greater than or equal to 1, and N0 = 1.
Click HERE for a GSP script of a Square Root Spiral.