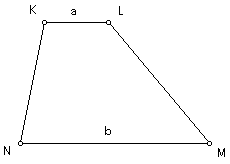
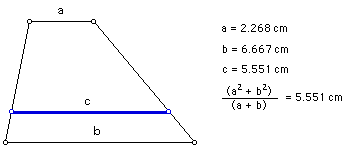Given trapezoid KLMN, with KL // NM, KL = a, and NM = b.
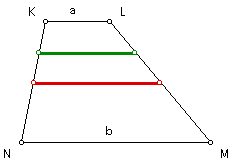
Construct the arithmetic mean segment (in red) and the harmonic mean segment (in green).
Construct the midpoint of the harmonic mean segment and call it point R. Construct a line perpendicular to the harmonic mean segment at point R. Construct the intersection of this line and the arithmetic mean segment and call it point S.
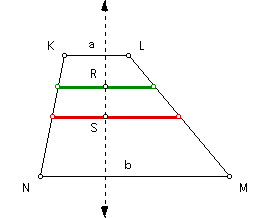
Construct a circle with center at point S and passing through point R. Construct the intersection of this circle with the above line and call it point T. Since SR and ST are radii of the same circle, then SR = ST.
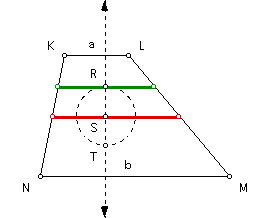
Construct a line parallel to base NM through point T. Construct the intersection of this line and leg KN and call it point P. Construct the intersection of the same line and leg LM and call it point Q.
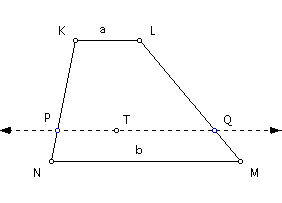
Construct segment PQ. The length of this segment is the contraharmonic mean, "c," of the bases KL and NM.
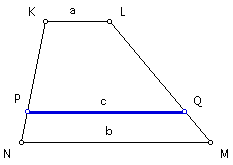
Double check the construction by taking measurements and using the equation for the contraharmonic mean.