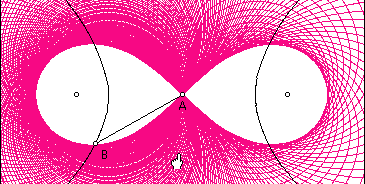Most trigonometry and pre-calculus students study graphs of polar equations. They know how to graph lines and circles on polar planes. The students also know the general forms of equations that will result in the graphs of limacons, cardioids, and lemniscates. And they know what these graphs look like and can graph them on a polar plane.
If you ask one of these students to construct a line or a circle in The Geometer's Sketchpad, if they've had experience with GSP, they can do it with ease. But try asking them to construct a limacon, cardioid, or lemniscate, and they probably have no idea. They may even think that it cannot be done. But it can!! This essay explains a couple of ways to construct these types of graphs in GSP.
Construct a circle and a point A outside the circle.
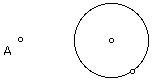
Construct a point B on the circle (NOT the one that was used to construct the circle). Construct segment AB.
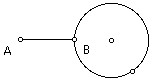
Construct a circle with center at point B and passing through point A.
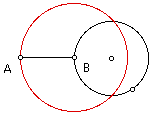
Construct the locus of this circle as point B moves around the first circle. The locus is a limacon with an extra loop!!

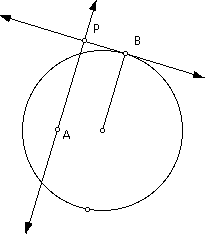
So how do you construct just the outline of the limacon with an extra loop? Start again with a circle, a point A outside the circle, and a point B on the circle (but NOT the one that was used to construct the circle).
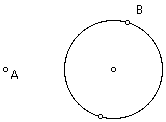
Construct a radius of the circle with point B as the endpoint on the circle. Construct a line perpendicular to this radius at point B (this line is tangent to the circle at point B).
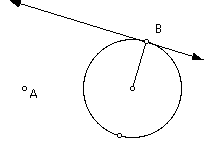
Construct a perpendicular line to the tangent line through point A. Call the intersection of this line and the tangent line point P. This point P is sometimes called the "pedal" of the circle.
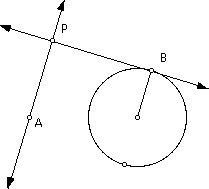
Construct the locus of point P as point B moves around the circle. The result is the limacon with an extra loop!
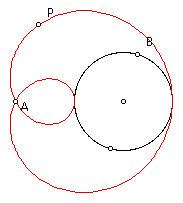
Construct a circle and a point A on the circle.
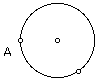
Construct a point B on the circle (NOT the one that was used to construct the circle). Construct segment AB.
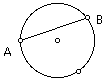
Construct a circle with center at point B and passing through point A.
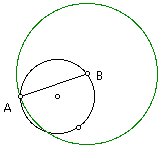
Construct the locus of this circle as point B moves around the first circle. The locus is a cardioid!!

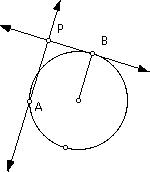
So how do you construct just the outline of the cardiod? Start again with a circle, a point A on the circle, and a point B on the circle (but NOT the one that was used to construct the circle).
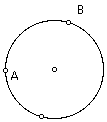
Construct a radius of the circle with point B as the endpoint on the circle. Construct a line perpendicular to this radius at point B (this line is tangent to the circle at point B).
Construct a perpendicular line to the tangent line through point A. Call the intersection of this line and the tangent line point P. This point P is sometimes called the "pedal" of the circle.
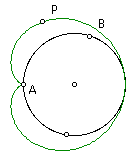
Construct the locus of point P as point B moves around the circle. The result is the cardioid!
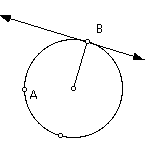
Construct a circle and a point A inside the circle.
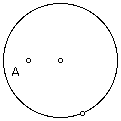
Construct a point B on the circle (NOT the one that was used to construct the circle). Construct segment AB.
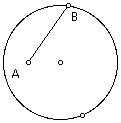
Construct a circle with center at point B and passing through point A.
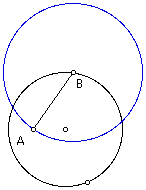
Construct the locus of this circle as point B moves around the first circle. The locus is a limacon without an extra loop!!

So how do you construct just the outline of the limacon without an extra loop? Start again with a circle, a point A inside the circle, and a point B on the circle (but NOT the one that was used to construct the circle).
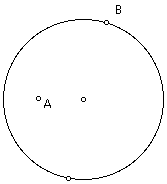
Construct a radius of the circle with point B as the endpoint on the circle. Construct a line perpendicular to this radius at point B (this line is tangent to the circle at point B).
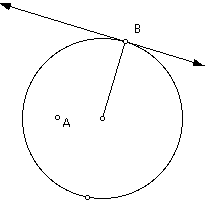
Construct a perpendicular line to the tangent line through point A. Call the intersection of this line and the tangent line point P. This point P is sometimes called the "pedal" of the circle.
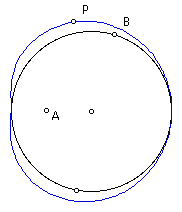
Construct the locus of point P as point B moves around the circle. The result is the limacon without an extra loop!
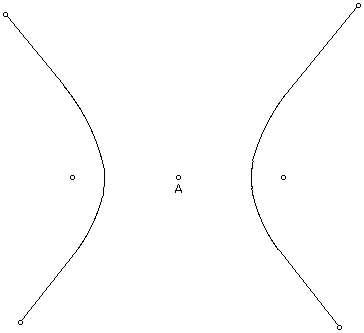
Construct a hyperbola and a point A at the center of the hyperbola.
Construct a point B on the hyperbola. Construct segment AB.

Construct a circle with center at point B and passing through point A.
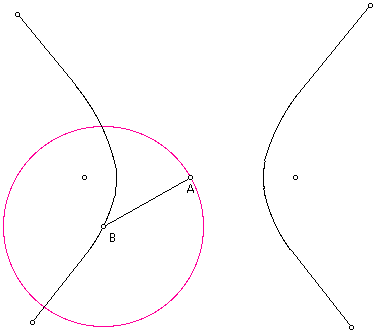
Construct the locus of this circle as point B moves around the hyperbola. The locus is a lemniscate!!