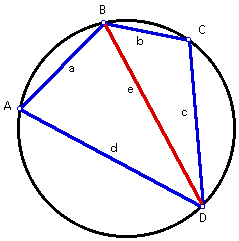
Given cyclic quadrilateral ABCD with sides of length a, b, c, and d. Let the length of diagonal BD be e. Let the angle between sides a and d have measure A, and let the angle between sides b and c have measure C.

Since quadrilateral ABCD is cyclic, then opposite angles A and C are supplementary (A + C = 180 degrees). Therefore, using trigonometry, cosA = -cosC, and sinA = sinC.
Using the Law of Cosines on the two triangles formed after constructing diagonal e, e2 = a2 + d2 - 2adcosA and e2 = b2 + c2 - 2bccosC. By transitivity, a2 + d2 - 2adcosA = b2 + c2 - 2bccosC. Since cosA = -cos C, then a2 + d2 - 2adcosA = b2 + c2 + 2bccosA. Therefore, a2 - b2 - c2 + d2 = 2(ad + bc)cosA. Squaring each side of the equation gives (a2 - b2 - c2 + d2)2 = 4(ad + bc)2*(cosA)2.
Using the trigonometric formula for finding the area of a triangle, and since the area of the quadrilateral is the sum of the area of the two triangles formed after constructing diagonal e, then the area of the quadrilateral equals (1/ 2)adsinA + (1/ 2)bcsinC. By substitution, Area = (1/ 2)adsinA + (1/ 2)bcsinA. Therefore, Area = (1/ 2)(ad + bc)sinA, and so 2*Area = (ad + bc)sinA. Multiplying both sides of the equation by 2 gives 4*Area = 2(ad + bc)sinA. Squaring both sides of the equation gives 16(Area)2 = 4(ad + bc)2*(sinA)2.
By the addition property of equality, (a2 - b2 - c2 + d2)2 + 16(Area)2 = 4(ad + bc)2*(cosA)2 + 4(ad + bc)2*(sinA)2. Factoring on the right side of the equation gives (a2 - b2 - c2 + d2)2 + 16(Area)2 = 4(ad + bc)2*[(cosA)2 + (sinA)2]. Substituting the trigonometric identity (sinA)2 + (cosA)2 = 1 gives (a2 - b2 - c2 + d2)2 + 16(Area)2 = 4(ad + bc)2. Therefore, 16(Area)2 = 4(ad + bc)2 - (a2 - b2 - c2 + d2)2. Note: For the rest of the proof, let A represent the area of the quadrilateral.
Factoring the right side of the equation gives 16A2 = [2(ad + bc) + (a2 - b2 - c2 + d2)]*[2(ad + bc) - (a2 - b2 - c2 + d2)]. After a little regrouping, 16A2 = [(a2 + 2ad + d2) - (b2 - 2bc + c2)]*[(b2 + 2bc + c2) - (a2 - 2ad + d2)]. After factoring again, 16A2 = [(a + d)2 - (b - c)2]*[(b + c)2 - (a - d)2]. Factoring once more gives 16A2 = [(a + d) + (b - c)]*[(a + d) - (b - c)]*[(b + c) + (a - d)]*[(b + c) - (a - d)]. Therefore, 16A2 = (a + b - c + d)(a - b + c + d)(a + b + c - d)(-a + b + c + d).
Since the semiperimeter of the above cyclic quadrilateral is defined as s = (a + b + c + d)/ 2, it follows that 2s = a + b + c + d, and so 2s - a = b + c + d. Adding -a to both sides of the equation gives 2s - 2a = -a + b + c + d. Therefore, 2(s - a) = -a + b + c + d. Similar algebra steps give 2(s - b) = (a - b + c + d), 2(s - c) = (a + b - c + d), and 2(s - d) = (a + b + c - d).
By substitution, 16A2 = [2(s - c)]*[2(s - b)]*[2(s - d)]*[2(s - a)]. After a little rearranging, 16A2 = 16(s - a)(s - b)(s - c)(s - d). Finally, A2 = (s - a)(s - b)(s - c)(s - d), and so A = [(s - a)(s - b)(s - c)(s - d)]1/2, which was to be proved. QED.