This is the write-up for problem #6 in assignment 1.

Graphs of the sine function

by

Doug Westmoreland

 

In order to analyze the effects that a, b ,c and d have on the graph y=asin(bx+c), let's first consider the graph of y=sinx.

The sine function is periodic with a period of 2 and amplitude of 1. Click here for a quick review of the terms periodic and amplitude.

The graph of y=sinx looks like this:

 

 

 

Now, let's analyze how the value of "a" effects the graph of y=asinx. Here are the graphs for y=asinx for a=1,2,3,4,5,6,7,and 8:

a=1 blue, a=2 purple, a=3 red, a=4 green, a=5 light blue, a=6 yellow, a=7 grey, a=8 black

We can see from these graphs that the "a" value effects the amplitude of the sine curve. We now can define that the amplitude of the sine curve of the form y=asinx is |a|.

Futher exploration: What if the values of "a" were negative? How would this effect the graph of y=asinx? Click here after you have thought about it.

 

 

Now let's examine how the value of "b" effects the graph of y=sinbx. The following graphs are for values of b=1,2,3,4,5

b=1 purple, b=2 red, b=3 blue, b=4 green, b=5 lt.blue

These graphs do get a little confusing in determining what the "b" value actually does to the graph of y=sinbx. To see a better presentation of the effects of "b" click here. After examining the graphs with variations of "b", we can conclude that the value effects the period of the function. We can now calculate the period of y=sinbx by dividing 2(pi) by b.

 

 

Now, let's take a look at how the "c" value effects the graph of y=sin(x+c). The following graphs are for values of c=-2,-1,0,1,2

c=-2 purple, c=-1 red, c=0 blue, c=1 green, c=2 lt.blie

 

One can see from these examples that the "c" value does not effect the amplitude or the period. What is does do is translates the graph of the equation y=sinx either right or left "c" units, depending on the value of "c". ( If "c" is positve, then the graph translates |c| units to the left. If "c" is negative, the the graph translates |c| units to the right.) This is called the phase shift of the sine curve. When the equation contains a "b" value other than 1, we can calculate the phase shift to be: -c/b.

 

 

 

Finally, let's take a look at a few examples of the combination of different values of "a" , "b", and "c" in the equation y=asin(bx+c) at the same time. The equation y=sinx (the blue curve) is used as a reference graph in each graph below.

 

y=2sin(3x-1)

 

y=-5sin(2x+3)

 

y=7sin(4x+3)

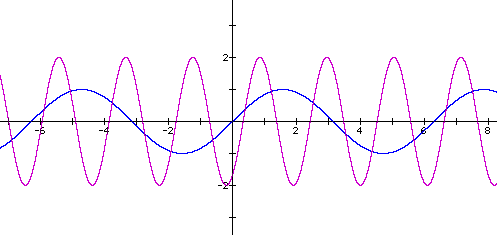
In summary, the values of a, b, and c in the equation y=asin(bx+c) either translates, reflects, dialates, and/or shifts the graph of y=sinx depending on the values of a, b, and c. In the write-up here, we can conclude that the "a" value effects the amplitude; the "b" value effects the period; and the "c" value effects the phase shift.

Amplitude=|a|

Period=(2pi)/b

Phase shift= -c/b

Return