Given: Three medians of a triangle

Prove: A) The medians are concurrent and B) The medians meet at a point whose distance from any vertex is two thirds the length of the median from that vertex.

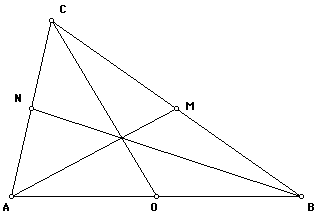
PROOF:

Part A

Let AM, BN, and CO denote the medians of triangle ABC.

The medians AM and BN intersect at some point Q.

Let point P denote the intersection of ray CQ and side AB.

There is a ray BX in the A-side of BC such that ray BX and ray MA are parallel.

Let point D denote the intersection of ray CQ and ray BX.

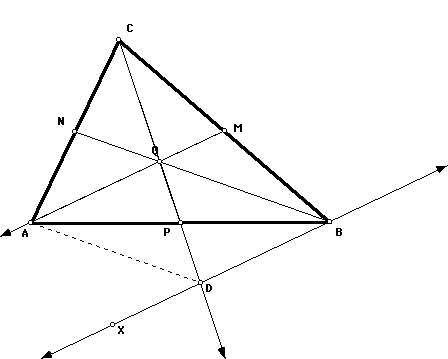
( For a more dynamic sketch that you can move around click here. )

In triangle CBD, MQ bisects one side and is parallel to a second side....THEREFORE, point Q is the midpoint of side CD.

Since NQ bisects two sides of triangle CAD, NQ is parallel to AD. THUS, the opposite sides of ADBQ are parallel and the figure is a parallelogram. Its diagonals bisect each other, so, point P is the midpoint of AB. THEREFORE point P and point O are the same point, which means that the medians are concurrent at point Q.

Part B

If the distance from point N to point Q equals y, then the distance from point A to point D equals 2y which also equals the distance from point Q to point B.

THEREFORE, the distance from point B to point Q equals two thirds the distance from point B to point N.

If the distance from point P to point Q equals x, then the distance from point Q to point D equals 2x, and , because point Q is the midpoint of CD, the distance from point Q to point C equals 2x. THUS, the distance from point C to point Q equals two thirds the distance from point C to point O.

In a similar fashion, it can be shown that the distance from point A to point Q equals two thirds the distance from point A to point M.