Part 1-- Review of write-ups 1 through 12. (Completed)

Part 2-- Write-up of the investigation below. (Completed)

Part 3--Course Evaluation (Completed)

Part 2

A. In this final write-up we will take a selected point P inside and outside a given triangle ABC and investigate some interesting relationships.

First, let's consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. See drawing below.

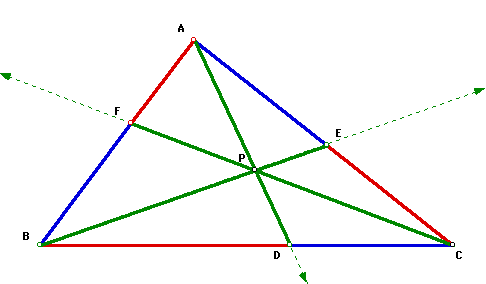
Let's now take a look at the products of the red segments and the products of the blue segments for various triangles and various locations of point P.

Click here for a GSP sketch that will allow you to change the size of the triangle and drag point P to different locations within triangle ABC. This GSP sketch is a full investigation of this first case when point P is inside trangle ABC.

After using the GSP sketch that was mentioned above, you should have observed that the products of the red segments appear to be equal to the product of the blue segments for various locations of point P and various sizes of triangle ABC. Therefore, if our conjecture is that the products are indeed the same, then the ratio of the red segments to the blue segments will always be equal to 1.

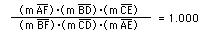
B. Now, no amount of dragging point P around or changing the size of the triangle in a GSP sketch will prove that the ratio is 1. Therefore, we need to prove this ratio above is indeed equal to 1. Let's consider our original sketch but let's draw some parallel lines to help produce some similar triangles. See the drawing below.

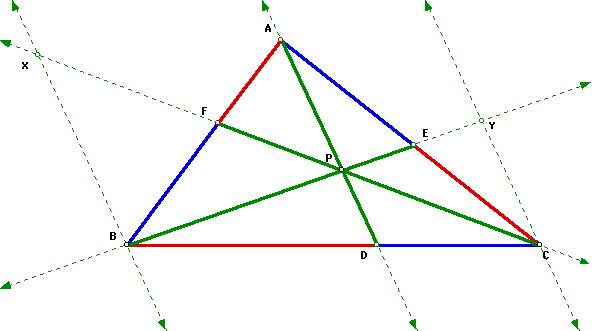
1.Triangle BXF is similar to triangle APF by AA similarity ...(Angle BFX is congruent to angle AFP...vertical angles are congruent; angle XBF is congruent to angle FAP...if 2 parallel lines are cut by a transversal, then the alternate interior angles are congruent)

2. Thus, BF/AF=BX/AP which leads to BX=((BF)(AP))/AF ..(if 2 triangles are similar, then the corresponding sides are in proportion)

3.Triangle APE is similar to triangle CYE by AA similarity ...(Angle AEP is congruent to angle YEC...vertical angles are congruent; angle APE is congruent to angle CYE...if 2 parallel lines are cut by a transversal, then the alternate interior angles are congruent)

4. Thus, AE/CE=AP/CY which leads to CY=((AP)(CE))/AE ..(if 2 triangles are similar, then the corresponding sides are in proportion)

5. Triangle CPD is similar to triangle CXB by AA similarity ...(Angle BXC is congruent angle DPC, and angle XBC is congruent to angle PDC....if 2 parallel lines are cut by a transversal, then the corresponding angles are congruent)

6. Thus, CD/CB=DP/BX which leads to (CD)(BX)=(CB)(PD) ..(if 2 triangles are similar, then the corresponding sides are in proportion)

7. Triangle BCY is similar to triangle BDP by AA similarity ...(Angle BCY is congruent to angle BDP, and angle BYC is congruent to angle BPD.....if 2 parallel lines are cut by a transversal, then the corresponding angles are congruent)

8. Thus, DB/CB=DP/CY which leads to (DB)(CY)=(CB)(DP) ..(if 2 triangles are similar, then the corresponding sides are in proportion)

9. (CD)(BX)=(DB)(YC) ...(substitution.....from statement 6 and 8)

10. (CD)((BF)(AP))/AF=(DB)((AP)(CE))/AE ...(substitution.....from statements 2 and 4)

11. (CD)(BF)(AE)=(DB)(CE)(AF) ...(Divide both sides of equation in statement 10 by AP and multiply both sides by (AF)(AE))

12. (AF)(BD)(CE)=(BF)(CD)(AE) .....(symmetry)

Can this result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle? Click here to see a GSP sketch where point P is outside the triangle.

C. In this final part we need to show that when point P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?

Example:

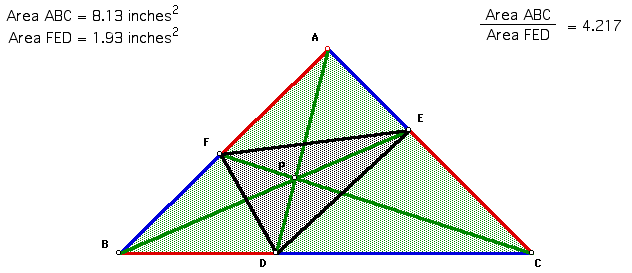
Click here for a GSP sketch that will allow you to drag point P around inside triangle ABC and observe the ratio of the areas of triangle ABC to triangle DEF.