

Lesson Investigation 1:
Construct a circle using either traditional construction tools or Geometer's Sketchpad. Label its center P. Use a compass to construct two congruent chords. Label the chords AB and CD as shown in the figure below. Construct the radii AP, BP, CP, and DP. Use a protractor to measure the central angles APB and CPD. What can you conclude?
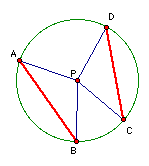
From this investigation, you may have discovered that the central angles (and, by definition, their arcs) are congruent. The result is summarized in the following theorem:
In the same circle or in congruent circles: (1) congruent chords have congruent arcs and (2) congruent arcs have congruent chords.
Lesson Investigation 2:
Construct a circle using construction tools or Geometer's Sketchpad. Label its center P. Draw a chord that is not a diameter. Label it AB. Construct the line perpendicular to segment AB through P. Label the point of intersection of this line and segment AB as C. Use a compass to compare the lengths of segment AC and segment BC. Compare your results with others in the class. What can you conclude?
From this investigation, you may have discovered that the lengths of AC and BC are the same. The result is summarized in the following theorem:
A diameter that is perpendicular to a chord bisects the chord and its arc.
Lesson Investigation 3:
Construct a large circle and mark the center. Construct two nonparallel chords that are not diameters. Construct the perpendicular bisector of each chord and extend the bisectors until they intersect. What is special about this point of intersection? Compare your results with other memebers of the class. Make a conjecture.
Upon futher investigation you should discover the following:
In the same circle or in congruent circles: (1) congruent chords are equally distant from the center (or centers) and (2) chords equally distant from the centers (or centers) are congruent.
If a chord is a perpendicular bisector of another chord, then the first chord is a diameter.
Click here to go to Chord Properties Student Exercises.