

An arc is an unbroken part of a circle. See Lesson 1 on circles for all the definitions associated with arcs.
A central angle of a circle is an angle with its vertex at the center of the circle. A central angle that intersects a minor arc at is endpoints is called the central angle of that arc. The measure of a minor arc is defined to be the measure of its central angle.

The measure of a semicircle is 180 degrees. The measure of a major arc will always be greater than 180 degrees.
Adjacent non-overlapping arcs of a circle are arcs that have exactly one point in common.
Arc Addition Postulate: The measure of the arc formed by two non-overlapping arcs is the sum of the measures of these two arcs.
Congruent arcs are arcs, in the same circle or in congruent circles, that have equal measures.
Theorem: In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent.
An inscribed angle is an angle whose vertex is on the circle and whose sides contain chords of the circle.
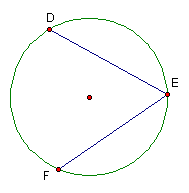
Click here for an INTERMATH description of inscribed angle. To return back to this page just click back on your browser while at the INTERMATH site.
Lesson Investigation 1: Construct a circle. Label its center P. Use a straightedge to draw a central angle. Label it angle RPS. Locate three points on circle P and label them T, U, and V. Use a straightedge to draw the inscribed angles RTS, RUS, and RYS. Use your protractor to measure all four angles. What can you conclude?
Try doing the same investigation above using Geometer's Sketchpad.
The previous investigation leads to the following theorem:
Theorem: If an angle is inscribed in a circle, then its measure is half the measure of its intercepted arc.
Take a look at the following theorems and do some investigations on your own using either Geometer's Sketchpad or tradition construction tools to confirm the conclusions. Can you prove them?
Theorem: If two inscribed angles of a circle intercept the same arc, the angles are congruent.
Theorem: An angle that is inscribed in a circle is a right angle if and only if its corresponding arc is a semicircle.
Theorem: A quadrilateral can be inscribed in a circle if and only if its opposite angles are supplementary.
There are other angle relationships in the circle involving chords, tangent lines, and secant lines.
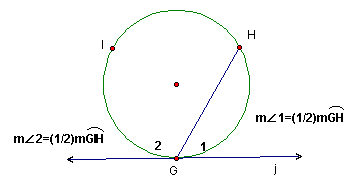
Theorem: If a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is half the measure of its intercepted arc.
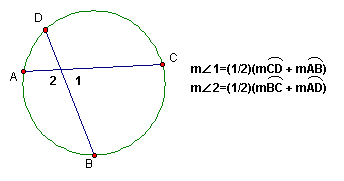
Theorem: If two chords intersect in the interior of a circle, then the measure of each angle is half the sum of the measures of the arcs intercepted by the angle and its vertical angle.
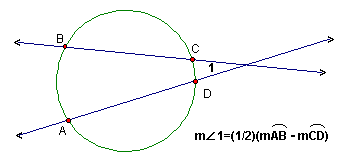
Theorem: If a tangent and a secant, two tangents, or two secants intersect in the exterior of a circle, then the measure of the angle formed is half the difference of the measures of the intercepted arcs.
Click here for more investigations and student exercises.