

Lesson Investigations
In this investigation, you will explore relationships between lengths of segments of intersecting chords and secants.
Investigation #1: Use Geometer's sketchpad to draw a circle with two chords that intersect in the interior of the circle. Each chord is divided into two segments. Measure each segment and find a relationship between them. (Hint: experiment with proportions)
Result of Investigation #1: In the figure below, chords AB and JK intersect at X. The lengths of the segments' four smaller segments are as follows:
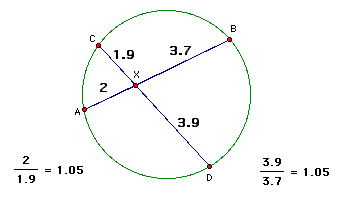
After experimenting around with the numbers you will discover that they form a proportion in the following way:
AX / CX = DX / BX
This is equivalent to (AX)(BX) = (CX)(DX).
The investigation results into the following theorem:
If two chords intersect inside a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segment of the other chord.
(Try to prove this theorem by similar triangles.)
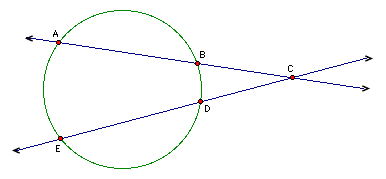
Investigation #2: Use Geometer's sketchpad to draw a circle. Then draw two secants that intersect in a point in the circle's exterior. Label the points as shown below. Find the measures of segments AC, BC, CD, and CE. Describe a relationship among these four measures.
Click here for student exercises.