EMAT 8990

by

Doug Westmoreland

Cyclic Quadrilaterals

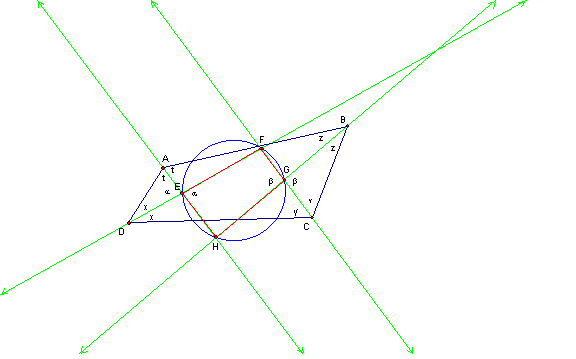
(Figure 1)

Given quadrilateral ABCD.  (figure 1 above)

Consider the following:  The four angle-bisectors of a quadrilateral always determine a cyclic quadrilateral.

Quick check:  a = 180 - ( x + t )  and b = 180 - ( y + z )

                      therefore   a + b = 360 - ( x + y + z + t )

                                                 =  360 - 180

                                                 = 180

So,  quadrilateral EFGH is a cyclic quadrilateral.

Click here for a GSP sketch of a cyclic quadrilateral that you can drag around and investigate.

Try dragging the vertices of quadrilateral ABCD so that the quadrilateral is a parallelogram.  What do you think about the cyclic quadrilateral that is formed?  If it is a special type of quadrilateral, can you prove the special case?

Further investigations on the cyclic quadrilateral

Consider this:

The four lines, each drawn from the midpoint of a side of a cyclic quadrilateral perpendicular to the opposite side, are concurrent.     Can you prove this?  Are there any special cases to consider?

Click here for a GSP model to investigate.

-------------------------------------------------------

Consider this:

Brahmagupta's Theorem:  In a cyclic quadrilateral having perpendicular diagonals, the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side.

Note: Brahmagupta was a Hindu mathematician 628 A.D. The position of the anticenter, the point of intersection of the diagonals of the cyclic quadrilateral, in the particular case of a cyclic quadrilateral with perpendicular diagonals was the discovery of Brahmagupta.

Click here for a GSP model to investigate.

Can you prove Brahmagupta's Theorem?  Click here for a hint.

Investigations on your own

Use GSP to make sketches of the following situations and see if you can prove them.

• In a cyclic quadrilateral with perpendicular diagonals, the distance from the circumcenter to a side is just half the opposite side.

• Let the diagonals of cyclic quadrilateral ABCD meet at M and let their midpoints be E and F. Then the orthocenter of triangle EMF is the anticenter T of ABCD.

• Let P and Q be the midpoints of a pair of opposite sides, say AB and CD.  The centroid K of ABCD is not only the midpoint of PQ but is also the midpoint of the segment EF joining the midpoints of the diagonals.

Return to Home Page

Return to Mathematical Gem Page