EMAT 8890

Doug Westmoreland

Proof:

Leave out FZ and denote the intersection of DX and EY by point Q.

Let AD meet BC at point T.

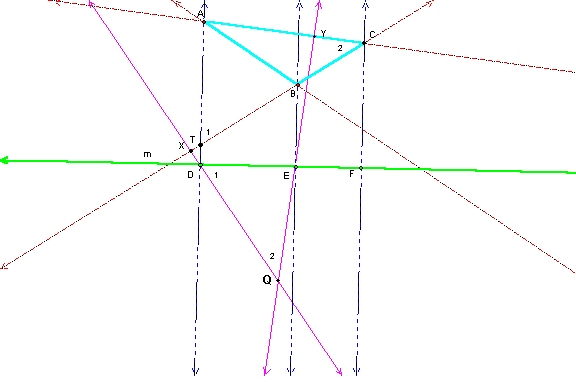
Then the sides of triangle TAC are perpendicular to the sides of triangle DEQ.  Therefore, triangles TAC and DEQ are similar.

Thus, angle C =  angle 2,  angle T = angle 1

and (AT / TC ) = ( DE / DQ ).

Now, start again leaving out the perpendicular EY, and let the intersection of DX and FZ be the point R.

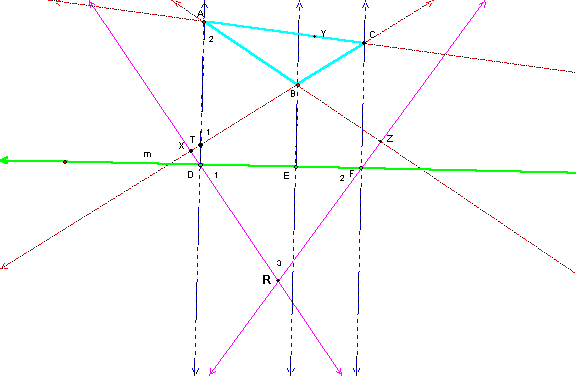
Then the triangles TAB and DFR have perpendicular sides and are similar.

So, ( TB / AT ) = ( DR / D F )

The parallels AD, BE, and CF give a third proportion:

( TC / TB ) = ( DF / DE ).

Multiplying these three proportions, you get the following:

( DE / DQ ) * ( DR / DF ) * ( DF / DE ) = ( AT / TC ) * ( TB / AT ) * ( TC / TB )

Therefore, ( DR / DQ ) = 1

Hence, DR = DQ.

Since both Q and R are on DX, Q and R are the same point.

Return