Department of Mathematics
J.Wilson, EMAT 6680

Lesson #12
by Jan White
This is an exploration of the length of piano strings
covering one octave in the upper range of my grand piano. I entered the
data in a spread sheet starting with the first string and numbering it
zero (first column) and the length (second column) and continuing for one
octave. I then took the ratio of the longer length divided by the next
smaller length and entered this in the third column. The fourth column
are the theoretical points from the function f(x)=10.4*(1.05296)^-a.
| String # | Length | Ratio | 10.4*Ave. Ratio^-a | |
| 0 | 10.4 | 1.05050505050505 | 10.4 | |
| 1 | 9.9 | 1.0531914893617 | 9.87691840145875 | |
| 2 | 9.4 | 1.0561797752809 | 9.38014587587254 | |
| 3 | 8.9 | 1.04705882352941 | 8.90835917401662 | |
| 4 | 8.5 | 1.04938271604938 | 8.46030160121621 | |
| 5 | 8.1 | 1.06578947368421 | 8.03477966989839 | |
| 6 | 7.6 | 1.04109589041096 | 7.63065992050827 | |
| 7 | 7.3 | 1.05797101449275 | 7.24686590232134 | |
| 8 | 6.9 | 1.06153846153846 | 6.88237530610976 | |
| 9 | 6.5 | 1.04838709677419 | 6.53621724102508 | |
| 10 | 6.2 | 1.05084745762712 | 6.20746964844351 | |
| 11 | 5.9 | 1.05357142857143 | 5.89525684588542 | |
| 12 | 5.6 |
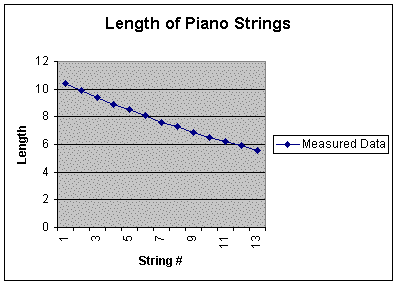
This first chart shows the measured data and that the
function is probably a exponential function.
This chart shows the measured data and the function, f(x)=10.4*(1.05296)^-a,
overlaid.