Department of Mathematics Education
J. Wilson, Emat 6680

Lesson # 4 – by Jan White

The CENTROID (G) of a triangle is the common intersection of the three medians.  A median of a triangle is the segment from a vertex to the midpoint of the opposite side.

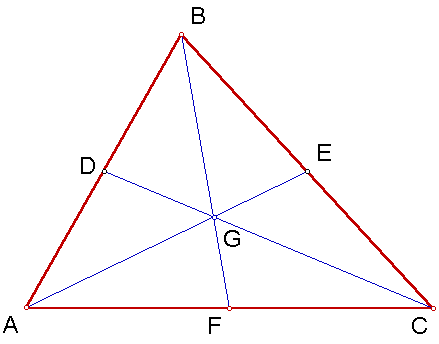
I will show that the centroid is 2/3 the distance from any vertex to the midpoint of the other side. (To see a more animated version click here. Does the relationship always hold?)

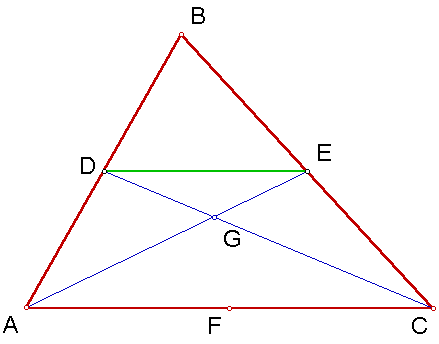
Let’s start by erasing the median BF and creating a segment DE.

AB/AD = CB/CE, therefore the new segment DE is parallel to segment AC.

Angle AGC=Angle DGE
Angle DEG=Angle GAC
Therefore triangle DGE is similar to triangle AGC.

By drawing a segment EF we can see that DE=AF and FE=AD. Since F is the midpoint of segment AC, DE/AC=1/2.

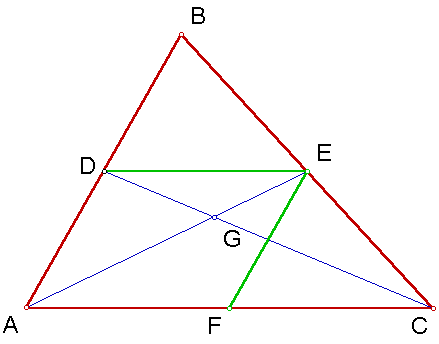
Looking back at the previous sketch DE/AC=DG/DC=EG/EA=1/2. Therefore G is 2/3 the distance from vertex A to side BC and vertex C to Side AB.  Similar reasoning can be used to show G is 2/3 the distance from vertex B to side AC.

RETURN