Department of Mathematics
J.Wilson, EMAT 6680

Assignment #7 Tangent Circles
By Jan White
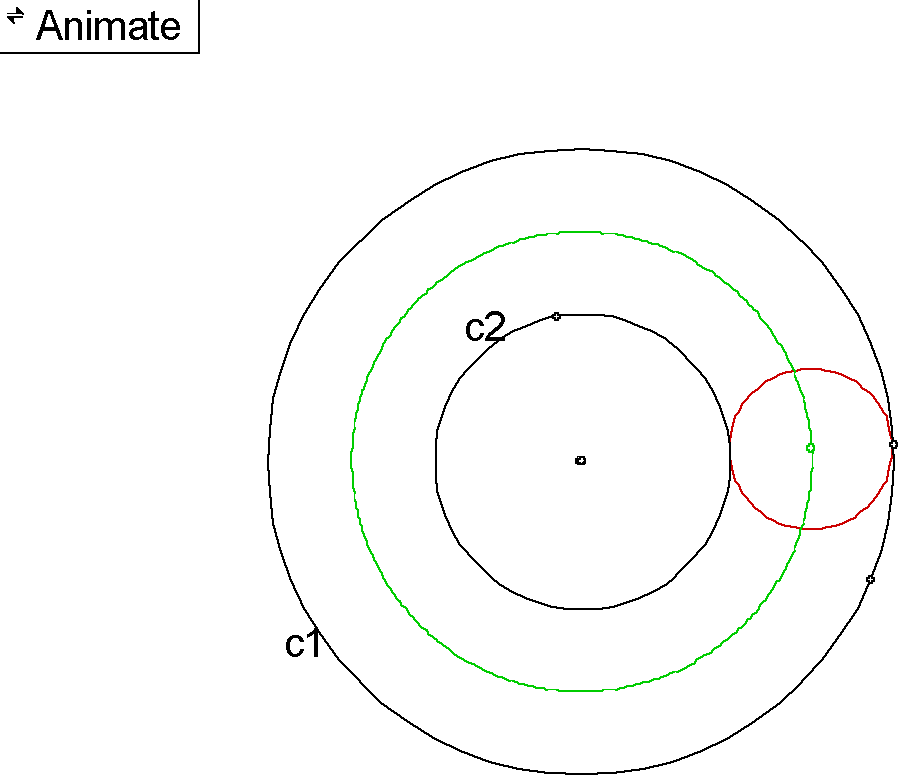
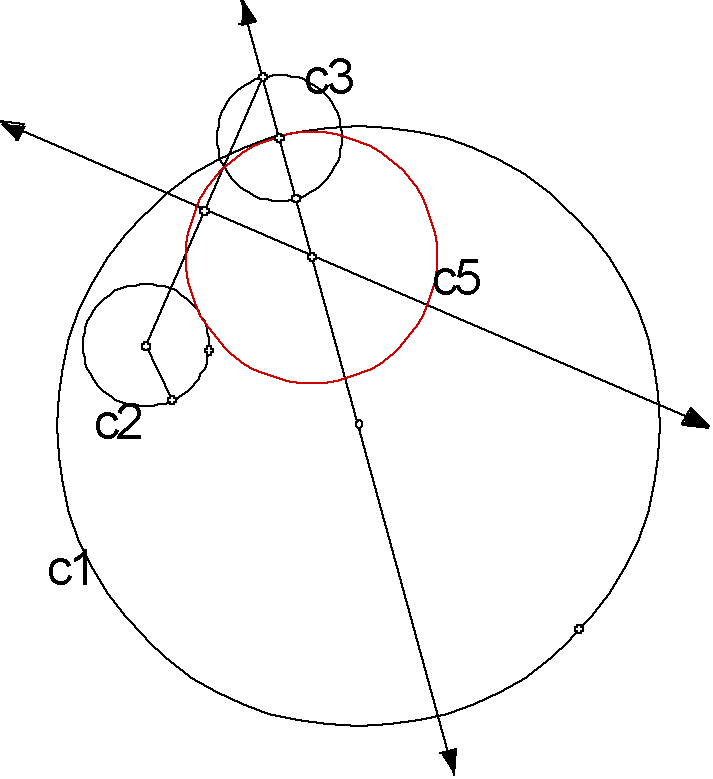
Given two circles c1 and c2 and a point on c1. Construct a circle tangent to the two circles with one point of tangency being the designated point. Construct a line through c1 using the center point and the chosen point on c1. Using the radius of c2 construct a circle,c3, with center at the given point on c1. Construct a segment connecting the center of c2 with the outside intersection of the line and c3. Find the midpoint of this segment and construct a perpendicular line at this point with the segment. Mark the intersection with this line and the line drawn through c1. Use this point and the center point of c3 as a radius for the tangent circle to both c1 and c2. This is the red circle in the design below.
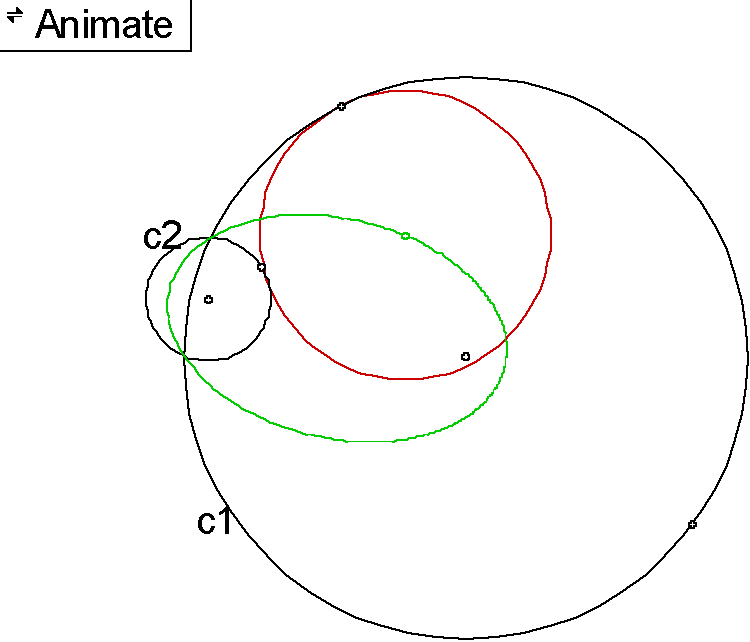
When we trace the center of this circle as the point of tangency with c1 moves around c1 the locus will trace an ellipse with the foci being the center point of c1 and c2. In case one where c2 is entirely within c1 and in case two where c2 intersects c1 in two places an ellipse will always occur.
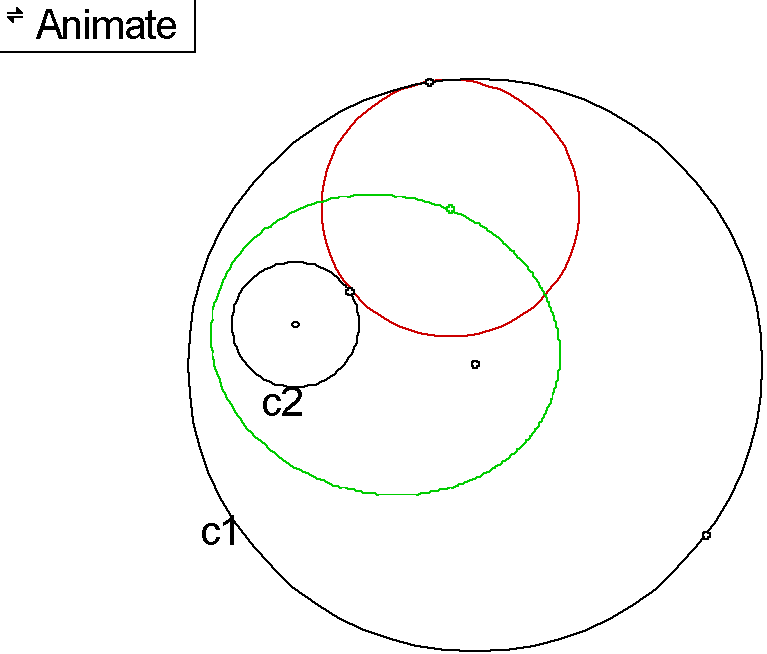
Press here for an animation
of case one.
Press here for an animation
of case two.
Case three is when c2 is entirely outside c1. The locus
of the center point of the tangent circle in this case defines a hyperbola.
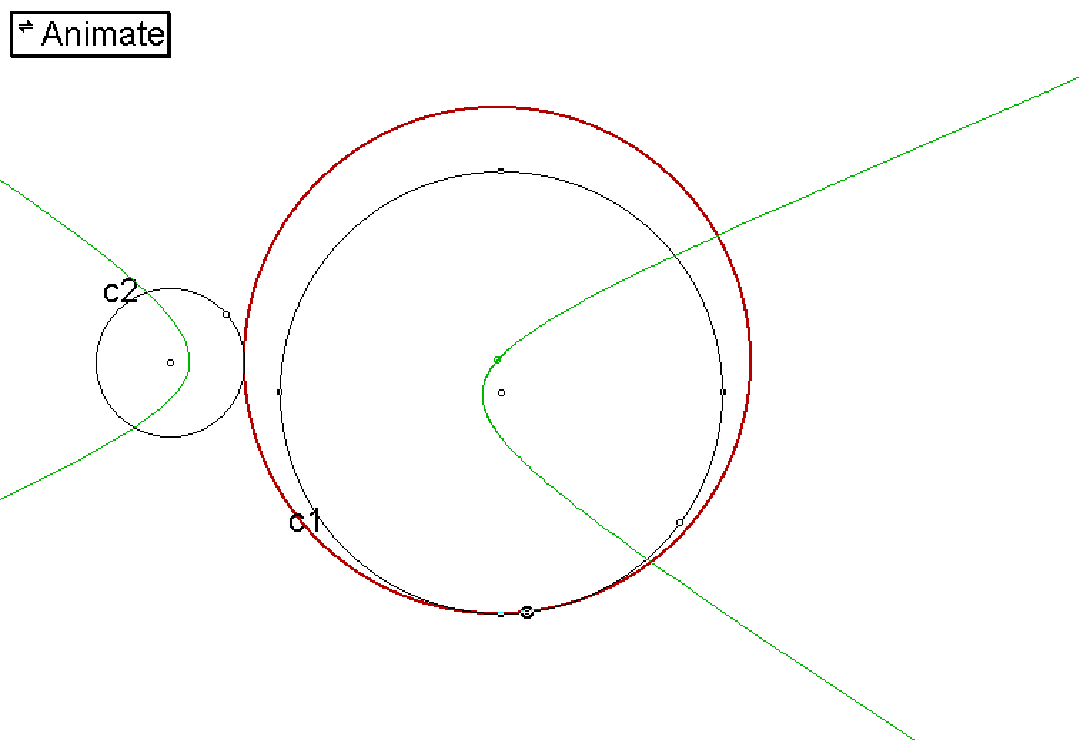
Press here for an animation of case three.
When the center of c1 and c2 coincide this will create a trace of a circle. (not very interesting but here it is)