

By using Geometer Sketch Pad we can explore this center of a triangle. The definition of the Circumcenter (C) we can construct the perpendicular bisectors of two different sides and then construct a point at their interscetion. Next we construct the circle by center and radius construction. And volla! we have the circumcenter and the circumcircle of our triangle (ABD).
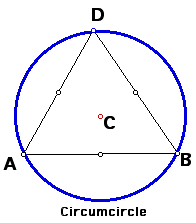
One interesting fact about the circumcenter can be observed by picking on vertex and moving it to create a new triangle. We will notice that C will move perpendicular to the opposite side of the triangle, no matter which vertex one picks.
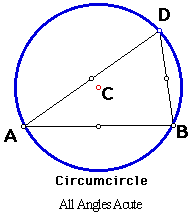
If we look at the movement of C, then we have to consider different types of triangles. First I checked to see when C is inside the triangle and when C is outside the triangle. Anytime that triangle ABD has all acute angles then the circumcenter C is always inside the triangle. When we have a right triangle then C is on the midpoint opposite the 90 degree angle. And when ABD is an obtuse triangle, or if triangle ABD has at least one obtuse angle then C will never be inside the triangle
.
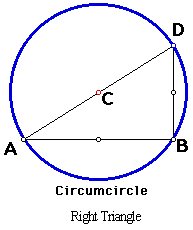
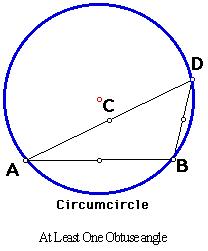
When we move the triangle around and if we trace the Circumcenter we will notice that C will move along the perpendicular bisector of the opposite side.
Give it a try and see what you can find out.