

We will start by constructing a simple triangle ABC and then constrtucting its orthocenter H.
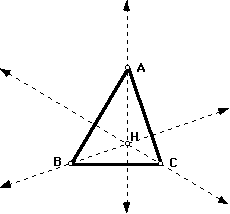
Now I want to construct the orthocenters (H2, H3, H4) of the other smaller triangles (i.e. AHC, BHC, BAH)
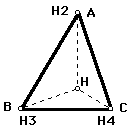
Here we notice that each of the orthocenters of the other triangles coinside with the original verticies of the triangle ABC.
Next we want to construct the Circumcircle of each triangle. (there will be 4 circles).
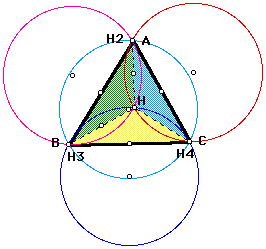
This image will help show each of the different parts that we have constructed. What do you notice? What would happen it we replaced H with A, B, or C?
Notice that when H lies on one of the verticies we have a right triangle. Also notice that the other two triangles dissapear.
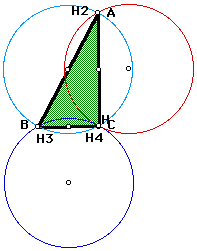
Do you notice anything about the circles? Take notice that
there are only three now. (Actually the pink and the light blue
are one top of one another.) The circle opposite C is now at the
same place as the centers of each circle move to the hypotenuse
of the triangle. This type of movement will be true for each of
the verticies as they exchange places with H.
Click here for an animation.