

In this assignment we will explore pedal triangles. First we want to construct a pedal triangle. Since we have a great library of GSP scripts we can just use them. However not everyone has a wonderful GSP library so we will revisit how to construct a pedal triangle. We will be constructing a pedal triangle from triangle ABC and any point p in the plane.
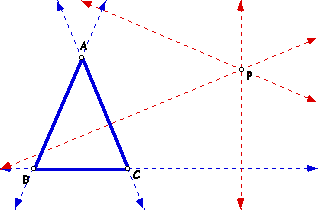
Next we will construct the perpendiculars from point p to each of the sides of the triangle. Note that depending on the triangle we may need to extend the sides so that the perpendiculars will intersect the lines.
The last thing we will do is make the pedal triangle itself. The points that we are interested in are the three intersections of the perpendiculars and the lines that go through the edges of triangle ABC. The Pedal triangle will be colored in green.
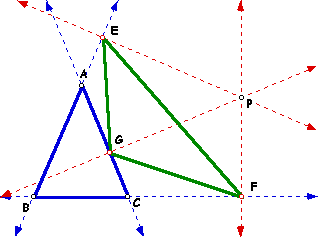
Thus now we have a pedal triangle EFG.
Click here to play with a working example in GSP, or click here for a script for the general construction of a pedal triangle to triangle ABC where P is any point in the plane of ABC.
What happens when if pedal point p is the centroid of triangle ABC?
Recall what the orthic triangle is. The orthic-triangle is made by connecting the feet of the perpendiculars.
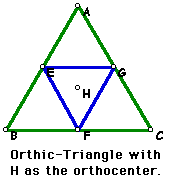
Well if we were to consider H as our P in the pedal triangle then our pedal triangle would be the exact one that we see here. Notice that if we were to constuct the perpendiculars to each of the sides then we will get E, F, and G. Since this is the way that we constructed them in the first place anyway. We can see this very easily when we constuct both on the same triangle.
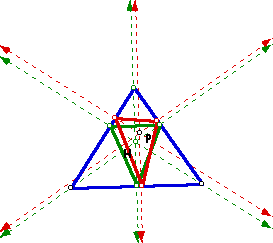
Notice as P approaches the orthocenter the triangles begin to line up. Also notice that the perpendiculars are beginning to line up as well.
Click here for an animation to see more clearly.