

#1. Graph
![]()
We can easily view this parametric equation using Graphing Calculator 3.0.
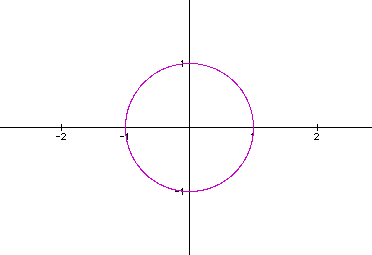
Anyone can observe that this graph is a circle. Now we want to try to explore different variations of this parametric equation.
We are going to replace x= cos (t) with x= cos(at). What do you think will happen. We will be varing the x coordinate of the parametric curve.
Notice when a is an integer (whole number).
Let a = 0
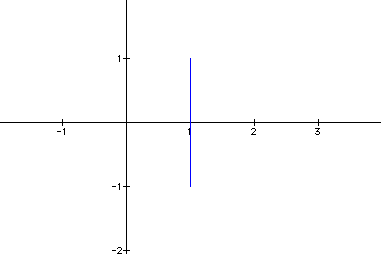
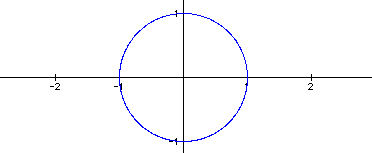
Let a = 1
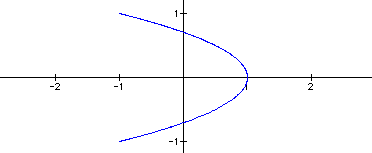
What about when a = 2?
a = 3?
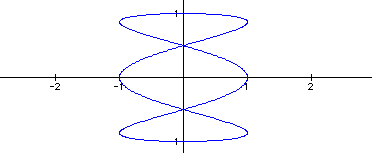
Click here to see a movie of the curve as a varies from -3 to 3. Just click on the play button next to the a at the bottom.
What do you notice? Observe that the open end moves back and forth along the x-axis from x= -1 to 1. Try to imagine that someone is twisting the y-axis and the curve is wrapping around it. Look at the movie again and see if you can see what I am describing?
Now let's focus on the other part of the parametric equation sin (t).
We know that when x= cos (t) and y= sin(t) we have a circle. We have already looked at varying t in the cos (t) by multiples of a. Now let's consider what would happen when we vary by a in the sin (t). My hypothesis is that just as we can see that the sin and cos functions are just shifted by one-half pi; the graph will be shifted by pi/2.
Just as before, we have the some of the same types of curves only this time they are rotated by 90 degrees. Let's look at the differences. When a= 2 the graphs are very different.
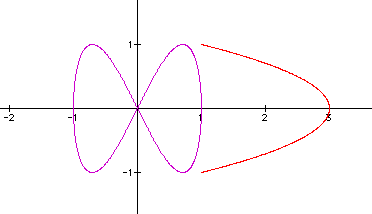
The next link has both graphs on the same axis. It is easier to see the similarities when x is an integer. Try to see how the graphs are similar. The red graph is the variation of the cosine part of the parametric equation plus a shift over 2 units so that we can compare the two at the same time. The purple is the variation of the sine part of the parametric equation.
With further observation one will notice that the graphs are not the same. It is true that they are rotated by 90 degrees, however, something else is happening. If we could look step by step we would notice that the red graph is where we altered the cosine part and left the sine alone. Thus at the beginning we can see the familar sine graph. The purple graph is where we altered the sine part and left the cosine alone. Just as before we can see the cosine graph at the beginning of the cycle (when a is between -.5 and .5).