

I begin my final project by constructing a triangle ABC and picking any point P inside the triangle. Next, construct the line that passes through the vertex and p and constuct the intersecting point on the opposite side.
We are posed with the following challenge:
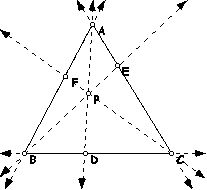
From my observations, I can see that the products are the same. (i.e. (AD)(BD)(EC) and (FB)(DC)(EA) are equal). So I set up an equation to make sure that what I had observed was not a special case. I found the ratio of the products and posted it on my GSP window. And as I expected the ratio is equal to 1.
Another interesting observation is that when a vertex is moved so that it lies on one of our constructed lines certain points and sides become equal.
See for yourself in GSP. The shaded areas represent the range of movement of the vertex where the other points still exist. Notice that when all three triangles are the same we have a equalateral triangle, and P is the orthocenter.